Вот сижу что-то ночью опять… Решил написать своё мнение о популярном сейчас вопросе: один или девять?
Я думаю, по изображению сверху стало уже понятно, о чём идёт речь. Знак умножения – он опущен перед скобками, и… как считать?
Посмотрим с двух позиций.
1) Знак умножения просто опущен. Тогда изначальная запись выражения выглядит так: 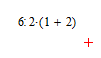 .
.
Шесть делим на два, умножаем на сумму единицы и двойки и (всё просто супер, детка) получаем девять. Ответ – 9. Вроде всё красиво, но…
2) Знак умножения не просто опущен. Как так – не просто? А просто так и нельзя опустить. Итак, вот есть инфа, которую, похоже, взяли из учебника за седьмой класс (изначальный источник не найден, но нагуглил в методичке какого-то математического лицея):
Случаи возможного пропуска знака умножения: 1) между буквенными множителями; 2) между числовым и буквенным множителем; 3) между множителем и скобкой; 4) между выражениями в скобках.
Что это для нас значит? А то, что если знак умножения опустили так, как описано в предыдущем пункте, то поступили неправильно, потому что двойка в примере – не множитель перед скобкой, а просто один из трёх множителей (если рассматривать деление как частный случай умножения). Поэтому, если он опущен правильно, то имеем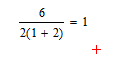 .
.
И это в том случае, если правило выше абсолютно точное. Но без конкретного источника (утверждается, что это школьный учебник) можно не рассчитывать на то, что оно точное. В школьной математике много требований, которыми даже в разделах вышки порой пренебрегают.
Это правило, к тому же, может оказаться неполным: вдруг нельзя опускать знак между скобкой и множителем в такой ситуации? Составлял бы я правила, я бы так и поступил. Спорная ситуация? Ставь ещё одну пару скобок! Будет вполне однозначно и всем понятно.
От себя скажу, что я часть после деления воспринимаю как нечто целое, т.е. скобку с множителем, мне это кажется вполне естественным. Почему же возникает спор? Многие запоминают, что «всегда можно опустить знак умножения». Но это не так. 2 умножить на 3 не есть 23, а произведение переменных c, o и s не всегда будет правильно понято.
На первый взгляд становится понятно, что человек, сказавший, что ответ – 1, просто забыл о порядке действий, его смутило отсутствие знака умножения. Здесь это чем-то напоминает мне загадку о ножках в комнате (где вопрос о том, сколько ног у животных в комнате. Вскользь упоминается, что ещё стоит и кровать. Если человек забыл про ножки кровати, он лох, если посчитал их, то тоже лох, ибо это не ноги, а ножки. Если посчитал ноги животных, то тоже лох, ибо у них лапы. Короче, вне зависимости от ответа человек – лох и ставит жирафа на аватар). А так как его действия (которые сначала нам показались такими) неправильные, то наше образование – говно и всё такое. Но если копнуть глубже, то действительно встаёт вопрос – а сколько? Если в реальной жизни в важном месте встретить такое, то, независимо от правильного ответа, нужно серьёзно поговорить с человеком, который написал это выражение и не уточнил, что он имел в виду.
Да, помню в какой-то методичке по экономике (у нас слабо вёлся этот предмет, и методички слабые были) была буквенная формула с такой же проблемой. Знак деления, справа большое достаточно выражение. Я тогда засомневался, в итоге нашёл правильную формулу. Да, там после деления всё должно было быть знаменателем. Но там это было однозначно неверно. Люди, пишите не правильно, а понятно 🙂
Однозначно 9.
Действия деления и умножения имеют одинаковый приоритет, дробной черты, отделяющей знаменатель от числителя, нет, дополнительных скобок нет, значит порядок: сложение, деление, умножение.
Но если воспринимать действие после деления , как целую часть, то ответ будет =1.
Вообще-то со времён школы выполняются сначала действия в скобках, затем умножения и деления слева направо поочерёдно, затем сложения и вычитания слева направо поочерёдно. пропущен знак умножения или нет — неважно, важно, что он понятен и присутствует. Деление (двоеточие) не то же самое, что дробная черта. Данное выражение можно было написать и как 6:2х3.
Сам пост читаем
ага
Сам пост читаем: между одним из множителей и скобкой.
=Умножение.
В случае умножения — то есть знак умножения просто опущен. Значит 9. Что в вашем посту, кроме не очень понятных выводов после приведенных вами же аргументов, говорит за 1?
Всё просто. Надо сделать проверку. Посчитать обратно. Только представим (1+2) как неизвестное. Пусть будет х.
Итак.
Если 6:2х=9
То 6=2х × 9
18х = 6
х = 6/18 = 1/3
Не подходит.
А если 6:2х=1
2х = 6
х = 3
Подходит (1+2) = 3
Значит правильный ответ основной задачи 1
Людмила, математик из вас не очень.
Как вы умудрились 2*х перенести в правую часть? Если уж переносить то получится что справа появится 2/x. 2 это делитель, то x это множитель. Получается всё с точностью до наоборот.
Данное выражение можно записать и так…
2 — это общий множитель…
6/ (2*1 + 2*2) ….
без скобок — не будет общего множителя
6/ 2*1 + 2*2, поэтому результат будет 1, а не 9
Тогда, 6/2*1=3, далее 3+2*2=7…..
???
Так записать нельзя!!!
Потому, что действие в скобках имеет главный приоритет.
Это если арифметика. А если алгебра? Там свои законы и правила расчётов, и тогда правильный ответ будет 1.
На всю математику одни законы без вариантов.
какая тут алгебра, если нет переменных???
Згоден!
https://www.facebook.com/photo/?fbid=3202723556685477&set=a.1415360708755113¬if_id=1688227101610375¬if_t=feedback_reaction_generic&ref=notif
А как же операция по раскрытию скобок, для чего они тогда нужны
как целую часть можно воспринимать если множитель 2 мы до этого вынесли из скобок как общий множитель. 6:(2+4). Но если мы выносим общий множитель за скобки то получается 6/2(1+2)=1 или если без дроби то 6:(2(1+2))=1. но в данном примере 6:2(1+2) ответ только 9
А как вообще появилась эта двойка за скобками ? Это общий множитель для 1 и 2 . Изначально было это было
2 и 4 и выглядело всё так
6 : ( 2 + 4 )=1
Взяли и вынесли общий множитель за скобки
6 : 2 (1+2) = 1
И что , от этого должен поменяться результат ?
2(1+2) это не просто скобки это блок и решать это надо блоково . Сначало надо вернуть этот множитель опять в скобки и только потом складывать .
Согласитесь , что эти 2и 4 взяли в скобки для того что бы начать действие со скобок . . При ответе 9 НЕ ИМЕЕТ ЗНАЧЕНИЕ НАЧНЁТЕ ВЫ СО СКОБОК ИЛИ ИМИ ЗАКОНЧИТЕ . Ответ будет одинаков и так и так . Получается скобки здесь совершено не нужны , их роль нулевая . И совсем другая картина при блоковом решении и ответе 1 . Этот факт есть косвеное доказательство — ответ 1 логичен . Если вы не начнёте решение с открытия скобок ответ будет другой . Введение в пример скобок обьяснимо и логично , при ответе 9 правило ,, начинать надо со скобок ,, не имеет смысла
Вот в том-то и дело, что блок один. А в случае 6:2(1+2) вы блок (2+4) превратили в два. 6, 2 и (1+2). Изначально же было всего два блока 6 и (2+4). По правилам это будет так 6: на блок (2+4). Соответственно, если вы хотите изменить что-то в блоке, то и заключайте этот блок в отдельные скобки: 6:( 2(1+2) ). Соответственно и результат не изменится.
Если при ответе 9 скобки не имеют смысла, тогда мы считаем просто слева направо, и получаем в итоге 5. Это математика. Тут нужны цифры , а не логика. Сначала скобки, потом всё слева направо.
«При ответе 9 НЕ ИМЕЕТ ЗНАЧЕНИЕ НАЧНЁТЕ ВЫ СО СКОБОК ИЛИ ИМИ ЗАКОНЧИТЕ .» — немного не верные мысли … это в данном примере так совпало, что 6/2 будет равняться тому что в скобках, т.е. 2+1, а если взять вот такой пример:
12:2(6-3)
6/6=6/(2+4)=6/(2*(1+2)).
Если уж преобразует единое выражение, то и показывайте, что это единое выражение, заключая его в скобки, а не записывая, как левая пятка захотела
А как это вы так лихо вынесли двойку и записали 6 : ( 2 + 4 )=1 в виде 6 : 2 (1+2) = 1 ?? Что за бред??
Если уж выносите, то и пишите правильно: 6 : ( 2 + 4 )=1 тождественно 6 🙁 2 (1+2)) = 1.
А 6 : 2 (1+2) = ДЕВЯТЬ!
Вот как нас вводят в заблуждение: https://hi-tech.mail.ru/news/61734-matematicheskaya-zadachka-slomala-mozg-amerikancev/?frommail=ft_ml
Лучше поздно, чем никогда)
Когда раскрываете скобки, не стоит левую часть делить
В данном примере если правильно раскрыть скобки, если уж решились на это, надо раскрывать их правильно так:
6:2(1+2)=6:2*1+6:2*2=3+6=9
Т.е. согласно вашей логике если 6/2х ответ будет 3х??? выражение в скобках (2+1) я заменил иксом — этого никто не запрещает, правда же? А заменил буквой как раз для наглядности того что ваше решение с ответом 9 — не верно. 6/2х= 3/х (получаем сокращением числителя и знаменателя на 2).
А вот 3х мы получим если изначальное выражение было бы записано как 6х/2 = 3х.
Но в задаче у нас 6/2х, а не 6х/2 — огромная разница.
Если до вас это дошло, то решаем дальше 3/х= 3/(1+2)= 1.
Ну и напоследок: знак умножения перед скобками опущен не случайно. Это алгебраическая задача. Не могу сюда прикрепить фотографию с выдержкой из учебника, но процитирую, не поленюсь:
«Порядок действий. В алгебре тот же порядок действий, что и в арифметике, но есть исключение: в алгебре знак умножения связывает компоненты сильнее , чем знак деления, поэтому знак умножения опускается. Пример, a:b*c = a:(b*c)»
Ссылки на то что эксель так считает или калькулятор не принимаются. Машина посчитает ровно так как оператор ей задаёт. А чтобы машина считала правильно, нужно записывать формулы и выражения с кучей скобок, выделяя для неё (машины) приоритет действий для вычисления. А за это отвечает оператор, который должен понимать что он считает.
Ежедневно приходится перегонять немало формул из советских пособий в эксель и ровно этим и заниматься — правописанием понятным для машины
Вы попутали знак деления со знаком дроби. Поэтому 6:2(1+2) не есть 6/2(1+2)
В інтернеті останнім часом сперечаються про порядок арифметичних дій .
І якщо з діями першого і другого СТУПЕНЯ все зрозуміло, то ДІЇ з дужками ( точніше ЧИСЛОМ ПЕРЕД ними) — викликають прям скажем — БАТАЛІЇ!
6/2(3 + 4) = 6/2(3 + 4)=6/(2*7)=0,42…
Чи
6/2(3 + 4) = 6/2*7=21…
Як бачимо тут ДВІ ВЕЛИКІ різниці!!!
Давайте спробуємо розібратися.
Почнемо з такого Варіанту:
Перевіремо:
2(2 * 3 + 2 * 4)=14
2(3+4)=14
ТУТ ВСЕ «ЗРОСЛОСЬ»
Тепер повертаємося до ПРИКЛАДУ ВИЩЕ:
6/2(3+4)=…???
З приведеного ВИЩЕ 2(3+4) ми бачимо ЩО РОЗРИВАТИ число перед дужками з числом в дужках НЕ МОЖНО, якщо між НИМИ не стоїть ніякий інший ЗНАК!!!
ТОМУ МАЄ ВИКОНУВАТИСЯ Правило: число перед Дужками ПРИВ’ЯЗЕНЕ ДО ДУЖОК, Якщо між ними не стоїть інший знак:
*, /, + чи — !!!!
Я розумію ЩО ХТОСЬ з великих ІДІОТІВ арифметиків — неДопрацював!!!
АЛЕ ТУТ ВИХОДИТЬ :
КАЗНІТЬ НІЗЬЗЯ ПОМІЛОВАТЬ
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Я не Матиматик АПРІОРІ
Але НУРОМ ВІДЧУВАЮ, що 0,5+0,5= ЛІТР ! 🙂
тогда вариант 3(1+2) почему не рассматриваете?
♂️
В качестве примера, где скрытое умножение обладает повышенным приоритетом по отношению к обычным умножению и делению можно считать «Курс теоретической физики» Ландау-Лифшица и другую физическую литературу.
Уточните на каких страницах «Теоретики» виден этот приоритет? (люблю проверять подобные факты в первоисточниках).
Т.е. статью вы не прочитали)) И математику в вузе не изучали. Учебники для 3го класса пишут люди с высшим математическим образованием. А эта задачка написана дурачками.
Тимофей, загляните в учебник 5 класса и там вам расскажут, что знак деления в виде двух точек АБСОЛЮТНО эквивалентен дробной черте.
Впрочем, весь цимус даже не этом.
Здесь работает другое правило — Распределительный закон умножения
k(m+n)=km+kn
А порядок действий, в общем виде, ЗВУЧИТ так:
Число деленное на произведение суммы!!!
С каких это пор знак деления равняется знаку дроби? Пятиклассник вы
Согласен, вопрос поставлен неправильно, опущен знак умножения, дополнительных скобок нет, горизонтальной черты нет, так что я воспринимаю это выражение как 6:2*(1+2)
иначе представьте вопрос: 1/2/3/4
(1/2):(3/4)
(1/2):3:4
1:(2/3):4
1:2:(3/4)
1:2:3:4
http://www.youtube.com/watch?v=JPe1aBW_YCg
Пусть это звучит глупо, я всегда (с тех пор как узнал об алгебре) рассматривал запись без знака умножения как «более тесную» связь между числами. Т.е. если a=3, то 6÷2a=6÷(2×a)=1, а не 6÷2×a=9. К сожалению, я не помню, было ли это взято из учебника или придумано мной, но умножение переменной на её коэффициент в алгебре должно выполняться раньше любых других операций, потому что это (простите за бурную отсебятину, пишу как понимаю) приведение чисел из алгебраического в арифметический вид. В случае со скобками я точно также воспринимаю число перед опущенным знаком умножения как коэффициент перед переменной.
Именно! Я тоже так считаю)
все так считают. Потому что умножение перед скобками считается первым (оно обычно не указывается и считается первым. Как будто там еще одни скобки стоят)
Правильный ответ 1
В том то и дело, что скобки еще одни не стоят!
Если мы берем пример 2:2(3-1), то в случае, когда 2(3-1) были бы знаменателем оно записывалось бы как 2:(2(3-1)), это неотъемлемая часть правила написания алгебраического выражения.
Вы не чего не забыли 2:2(3-1)=2:(2*(3-1)≠2:2*(3-1)
Всё правильно, правильный ответ 1
а — неизвестное, не сравнивай.
У тебя ОЧЕНЬ бурная отсебятина 🙂
Правильный ответ 1
Перед скобками знак умножения просто не пишется но имеется ввиду что он есть
В случае с 2а все равно подразумевается знак умножения, и все равно действия идут слева направо. Проверьте себя любыми школьными примерами и поймёте. 😉
Тогда решите пример 655, 3) из Сборника задач по алгебре для 6-7 классов, П.А. Ларичева.
Ссылку прилагаю, ответ в задачнике есть.
https://russianclassicalschool.ru/biblio/13_sr_sk_uceb_algebra.pdf
Милый мой где же Вы в данном выражении 6:2(1+2) нашли a, x, b или хотя-бы с что бы иметь право ссылаться на литературу 1952 года выпуска где к тому же не дано объяснение решения?
А Вы, ненаглядный мой, примеры 6:2(1+2) и 6:2(а+2) будете решать по-разному?
Считаю, что ответ 1, т.к. в 2(1+2) двойка за скобкой это общий множитель, так учили в школе (выпуск 2000г.). В примере 655, 3) ответ у меня сошелся с методичкой
Бегом в школу изучать что такое множитель. Тут множитель 6:2.
Вы совершенно правы!Благодаря Вашему объяснению я нашла подтверждение своей уверенности в правоте своего мнения.
Молодец!
Так и есть. Выражение 6:2а читается, как «6 делим на 2а».
Да дело то совсем не в более тесной связи, а распределительном законе умножения — a(b+c)=ab+ac.
Из которого следует, что множитель лишь визуально вынесен за скобку, в РЕАЛЬНОСТИ же относится именно к тому, что находится внутри скобок.
Распределительный закон умножения не об эквивалентности записей, тем более в выражении, а о том, как следует вычислять произведение числа на сумму чисел.
2*(1+2) действительно равно 6, но выражение 6:2*(1+2) несколько длиннее, если вы не заметили, и вычисляется в соответствии с правилами последовательности вычисления выражений независимо от того, чем обозначена операция умножения — символом или его отсутствием.
Если же 6:2*(1+2) не равно 6:2(1+2), то получается что 2*(1+2) не равно 2(1+2), что неверно.
здесь нет переменной
Полностью согласна с вами. Советская школа учила мыслить логически.
Пост, конечно, старый, но я все же про комментирую. Вот у автора серенькая плашечка, так называемая выдержка из учебника, со случаями возможного пропуска знака умножения, и там третий пункт должен развеять все сомнения: это как раз наш пример, когда знак умножения пропущен между множителем и скобкой. Не знаю, как в школах учат сейчас, но в далеком 98-м году, когда я училась в седьмом классе речи о приоритетности правой части уравнения над левой рассматривалось только в случае ограничивания этой самой части скобками. И только в этом случае.
Нет никаких «но» и «вдруг»: в данном конкретном примере пропуск знака умножения допустим, и выражение необходимо читать, как 2*(1+2).
Я знаю, что вас смущает. Можно сравнить это с визуальной иллюзией, ведь внешне и без знака умножения часть 2(1+2), «на глаз» так сказать, воспринимается действительно, как единое целое, которое психологически хочется увести в знаменатель полностью.
что мы имеем в итоге, считая последовательно слева направо с учетом отдельно вычисляющейся суммы в скобках: 1-й множитель 6/2 (шесть вторых) и 2-й множитель (1+2) . Ну и считаем их произведение. Получаем 9. А методичку сожгите.)
Ваша учительница по математике перевернуламь в гробу.
Ваша учительница по русскому языку сделала то же самое.
6:2(2+1) ≠ 6:2*(2+1)
Верно ?
Те, кто учился по советским методичкам, создали ядерную бомбу атомный ледокол, запустили человека в космос. Кстати без современных калькуляторов, которые дают на этот пример ответ 9. Я закончила советскую школу, и поэтому мой ответ: 1. 2(1+2) — это общий множитель, относящийся к скобке, и внеся этот множитель в скобки, получим (2+4) =6
6:6 =1. Не нужно охаивать старую математическую школу. Через 10-20 лет, у всех в этом примере ответ будет 9, а пока есть два лагеря.
Безусловно, ответ :1. Согласна с вашим комментом на все 100%!!! Особенно про космос и ответе — «9»на задачу в дальнейшем. Нет логики, а отсюда и глубоких знаний! Егэ выполнил своё предназначение!
Для единицы исходник должен выглядеть так:
6:(2(1+2))
Исходный материал был 6 : ( 2 +4 ) =:
Из (2+4) вынесли общий множитель 2 за скобку …. и что , от этого он стал ,, жить самостоятельной жизнью ,, ?
А как 6:(2+4) превратилось в 6:2(1+2)?
давайте тогда 3(1+2) рассмотрим
Браво!!! Кратко, ёмко! Ответ: 1, конечно же!
НЕТ.
Ну если вы, конечно, не отменили Распределительный закон умножения!
Лучше прочитайте правила раскрытия скобок « a(b+c) =ab+ac
Советские дети были гораздо умнее современных и им не нужны были дополнительные скобки, они и без них всё понимали. Ответ у людей с советским образованием 1, а у ЕГЭшников — 9.
Это конечно все хорошо…но как тогда решать простейшее выражение??? 8:2( а+с). На протяжении 6 лет, нас учили раскрыть скобки: 8:2а+2с! И в этом случаи результаты будут иметь разные значения… интересно было бы узнать мнение профа!)))
ничего подобного, максимум что может быть это 8:(2а+2с), поэтому удобнее и правильнее было бы записать данный пример, как 4(а+с).
8:2( а+с) = 8:2а+8:2с
я просто в ахуе.. куда катится мир
в примере 8:2(а+с) будет ответ 4а+4с, никак не может один делитель делить 8, а второй стоять отдельно в сумме.
8:2(а+с)=4(а+с)=4а+4с
Такой ответ будет, если мы хотим получить Четверку. А если хотим Пятерку (отлично), то ответ 4(а+с)
В вашем случае скобки раскрываются так: 8:2а + 8:2с
4(а+с)
блин, вы чо все с дуба рухнули? Если у вас так туго с арифметикой запустите excel или калькулятор виндовый, перевидите в инженерный, там есть скобки и посчитайте. Уж в мелкософте не довны работают, они то в отличие от вас точно знают как правильно это по считать. ответ 9 если чо.
В том то и дело, что калькуляторы дают разные ответы
Мой CITIZEN SRP-285N (22Eur — самый дорогой что был в магазине) решает так:
6/2(2+1)=1
6/2*(2+1)=9
Вот и спорь теперь с ним 😀
NB! Кст, попробуй Windows’кий калькулятор. Там вообще свою тему прёт, если * не ставить 😀
я пробовал считать в эксэле результат такой:
когда я набрал в ячейке =6/2(1+2)
он мне написал что там не хватает умножения.
«Приложение Microsoft Excel обнаружило ошибки во введенной формуле. Принять предполагаемые исправления?
=6/2*(1+2)»
То есть он САМ исправляет. САМ ставит там знак умножения. И тогда результат будет 9. Без знака умножения не считает.
Этот калькулятор явно интерпретирует косую в качестве знака деления как горизонтальную, обозначающую деление. В первом случае ему не хватает причин отделять под чертой скобку от двойки. Это ошибка программистов, которые «обували» этот калькулятор. Косая в качестве знака деления должна интерпретироваться как в языках программирования, — так же как двоеточие в школе.
Твой Сити Дзен довольно интеллигентный и правильно умеет читать. Объясняю : «/» это есть знак дроби. В первом случае твои сити видит все, что стоит после знака дроби 2(2+1) как делитель , а 6 — как делимое : 6/6 =1.
Во втором же случае твой дзен запись 6/2 видит как первый множитель , то есть 3, в произведении 3 × (2+1). Так что вон воченнь вумнай твой СитиДзен. Бери у него уроки
А если ещё скобки раскрыть или же двойку в скобки внести, ни кто не думал, что это мать ее, математика, наука черт знает о чем, абстракция, можно доказать что угодно
Если, что-то смущает, то надо видоизменить написание примера 6/2(2+1)=6/(2+1)2=1, потому что от перемены мест слагаемых и произведения результат не меняется, а вот деление другое дело и дробь и деление это одно и тоже. Всё, что стоит за знаком деления идет в знаменатель… так, что 6/6=1. А 9 получилось бы, если бы было написано так: (6/2)(2+1)=9 — и это уже произведение дроби и суммы. Решайте как написано, не надо придумывать….
Это математика, люди! А не психология…. здесь нет задач: типа автор думал, и кто во что горазд и т.д….. если записано так, значит и ответ такой, если написано иначе значит и ответ был бы другой.. А притягивать за уши, и логически рассуждать это чистой воды мошенничество и рассчитано на людей безграмотных…. В школе я училась давно, но видно хорошо меня учили….))))
Всем успехов!
>Всё, что стоит за знаком деления идет в знаменатель…
Схуяли?
>потому что от перемены мест слагаемых и произведения результат не меняется
Да, но деление стоит слева и у него приоритет, так что если хотите менять члены произведения местами, то будет так:
(2+1)*(6/2)
Ебанулись? Если бы было написано так 6/(2(2+1) то за деление ушло в знаменатель, а как в примере в знаменатель уйдет только 2
О боги, вы сейчас 1/2 превратили в 2, а 2+1 превратили в 1/(2+1)!!! Вы серьезно??? Иногда мне кажется, что люди на полном серьёзе пишут такие вещи, чтобы победить кого-то…. Чтобы сидел где-то аноним и думал: какие же вы тупыыыые!!!!!!! И фейспалмил с этого, а гнев выразить не на кого, потому что все в интернете…
!!!!!!!!!!!!!! Энгри смайлы.
Ага, как же, идёт всё в одну кучу. Обратитесь к математике и программированию. Чтобы после деления всё относилось к делителю — необходимо чтобы оно находилось в скобках. Ну и неприменимая теория про перестановку морганиях полный абсурд, давайте ещё 6 поменяем с 2, почему бы и нет
Есть разница между умножением со знаком и без знака. А разница состоит в том, что при умножении без знака произведение рассматривается как цельная величина. На бытовом примере: если 2а это литр жидкости, то 2×а это два пол-литра жидкости.
Рассмотрим пример:
2а:2а=1
при а=1+2
2(1+2):2(1+2)=6:2(1+2)=6:6=1
Для тех, кто не помнит этого правила, предлагаю решить пример на понимание. Для этого необходимо решить пример №797 из «Сборника задач по алгебре», Часть I, для 6-7 классов. (П.А. Ларичев) и сверить полученный результат с ответом. Сборник можно скачать в интернете бесплатно.
Нет сомнения, что те, кто сможет решить пример из Сборника, однозначно дадут правильный ответ на спорный пример:
6:2(1+2) = 1
Опускание знака умножения _опционально._ Его можно опускать, а можно не опускать. Это изменение _вида_ записи одного и того же выражения, а не операция, изменяющая способ его вычисления, а значит, потенциально, и значение. Это значит что пропущенный знак умножения должен трактоваться точно так же как указанный в явном виде.
Одночлен в алгебре определяется как готовое произведение составляющих его переменных и коэффициента, а не как выражение с опущенными знаками умножения, поэтому он является неделимым объектом. От любого другого алгебраического выражения одночлен отличается тем, что в нем невозможно просто заменить переменные на их значения. Это отдельная чисто алгебраическая сущность. Запись произведения числа или переменной на скобку не является одночленом независимо от того, указан знак умножения или опущен, поэтому, как и любое другое выражение, может изменить свой смысл в составе более крупного выражения.
Единственный здравый комментарий в куче ереси.
Послушайте. Число перед скобками определяет количество того, что в скобках. Объясню. У нас шестьдесят литров допустим пива. В скобках — одинарная порция. Выражение 60 : (5-2) = 20 значит, что одинарная порция составляет (5-2) = 3 литра. И хватит по одинарной порции на 20 бухариков. А выражение 60 : 2(5-2) = 10 значит, что по двойной порции хватит уже только 10 бухарикам. Т.к. выражение 2(5-2) — это уже двойная порция. Это то же, что и 60 : 2х. Когда опущен знак (умножить), то скобки теряют смысл. Это значит писать 60 : (2х)??? Короче, выражение 60 : 2(5-2) равно выражению 60 : (2*(5-2)). Когда в данном случае пользователь пытается восстановить специально опущенный знак «умножить» между множителем и скобкой, то следует восстановить и специально опущенные в таком случае скобки. Такова грамота писания математических выражений. И знак «умножить» и скобки опущены в данном случае прямо согласно грамоте писания математических выражений. Вот и все.
Правила раскрытия скобок, основаны на распределительном законе умножения:
a(b+c) = ab + acНа самом деле раскрытием скобок называют ту процедуру, когда общий множитель умножают на каждое слагаемое в скобках. В результате такого умножения скобки исчезают. Например, раскроем скобки в выражении 3×(4+5)3 × (4 + 5) = 3 × 4 + 3 × 5
Отсюда следует: 2(2+1) =2*2+2*1=6, 6:6=1
Но эта задача не для 4 класса, что и сбивает с толку
Вообще-то всё это есть в интернете
Законы умножения https://naobumium.info/arifmetika/umnojenie2.php
…………….
Есть формулы и про пиво и др. напитки
«ЛИГРЫЛ» http://alcoholclub.narod.ru/about/formula.html
Ну конечно, только почему же, раскрывая скобки, вы куда-то дели шестерку?
6/2(1+2) = 6/2*1+6/2*2= 3+6=9
Твой Сити Дзен довольно интеллигентный и правильно умеет читать. Объясняю : «/» это есть знак дроби. В первом случае твои сити видит все, что стоит после знака дроби 2(2+1) как делитель , а 6 — как делимое : 6/6 =1.
Во втором же случае твой дзен запись 6/2 видит как первый множитель , то есть 3, в произведении 3 × (2+1). Так что вон воченнь вумнай твой СитиДзен. Бери у него уроки
Говорили , нужен пруфф , который можно проверить . Вот https://resheba.ws/urok/matematika/05/001/067.html Скобки и действия с ними в приоритете, потом все остальное. Ответ 1.
В алгебре тот же порядок действий, что и в арифметике, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например, a:b·c= a: (b·c).
Этот текст из «Методики преподавания алгебры», курс лекций, Шустеф М. Ф., 1967 год. (стр. 43)
https://russianclassicalschool.ru/biblioteka/matematika.html
Поскольку в спорном примере знак умножения опущен, то спорный пример алгебраический.
Исходя из вышесказанного: 6:2(1+2) = 1
Но заявленная выше задача чисто арифметическая, почему вы в выражение без переменных пытаетесь буквы добавить?
Задача чисто алгебраическая, поскольку пропуск знака умножения — правило алгебраическое. «Алгебраическое выражение может не содержать чисел, обозначенных буквами».
Что же Вы не полностью процитировали абзац у товарища Шустефа М.В.?
Позволю продолжить:
«Для устранения недоразумений В. Л. Гончаров указывает, что предпочтительнее пользоваться в качестве знака деления чертой и ставить скобки [87]. П. С. Александров и А. Н. Колмогоров [59] предложили изменить порядок действий в арифметике и решать, например, так: 80:20*2=80:40=2 вместо обычного: 80:20*2=4Х2=8. Однако это предложение не нашло поддержки.»
Т.е. если уж и аппелировать к работе Шустефа М. Ф., то очевидно, что:
а) товарищ Гончаров указывает — пишите сразу понятно (тут все согласятся, т.к. вопрос оказался интересным);
б) если африфметика противопоставляется алгебре, то в нашем случае как раз имеет место «пример П. С. Александрова и А. Н. Колмогорова», и из того, как он подан у Шустефа М. Ф. понятно, что «обычно» пример с цифрами решается слева на право, а не отдавая приоритет умножению.
Поэтому так себе аргумент на самом деле.
Пропуск знака умножения это алгебраическое правило. Буквенное обозначение – не единственный признак алгебры. Поэтому спорный пример алгебраический и пропущенный знак умножения связывает компоненты сильнее, чем деление. Поэтому 6:2(1+2) = 1.
Что же касается предложения П. С. Александрова и А. Н. Колмогорова, которое не нашло поддержки, то поэтому, в случае если знак прописан, мы имеем: 6:2×(1+2)=9.
Прочитайте вслух выражение 8:2а
Каждый читает так, как решает. Я прочитаю вслух: “8 разделить на 2а”. А мой оппонент, который предлагал такой же метод, читал: “число 8 разделить на 2 и умножить на а”.
Вот давай теперь в твой пример подставим:
a = 2
b =2
c = 2
получаем:
2:2*2=2:(2*2) что в итоге 2:2*2 = 2:(4) и это по твоему правильно?
Чтобы получить 1 в исходном примере должна быть запись:
6:(2*(2+1)) и только так. Даже через переменные:
6:2(a+b) = 6:(1/2а + 1\2b)
Перемещая делитель внутрь скобок не забывайте делить то что внутри скобок на него а не умножать!
2:2*2=2:(2*2) Не верно поставлено равенство. Если знак умножения прописан, то 2:2*2 = 1×2 = 2.
2:(2*2) = 2:4 = 0,5.
Поскольку опущенный знак умножения связывает компоненты сильнее, чем деление, то в случае написания знака умножения мы имеем:
6:2(1+2) = 6:(2×(1+2)) = 6:(2×3) = 6:6 = 1.
Методика преподавания алгебры в восьмилетней школе, Репьев В. В., стр. 81
Не хочу вставить на чью либо сторону, но видел ваши сообщения на разных форумах и тема, как мне кажется вас сильно задела.
Во всех своих доказательствах вы опираетесь на тот факт, что данный пример является чисто алгебраическим, так как в нем было использовано алгебраическое правило опускания знака умножения.
В приведённой вами книге сказано:
В выражении, где имеются действия только одной ступени, вычисления ведутся в порядке записи действия.
Но в алгебре это правило не применяется в случае деления числа на произведение.
В правописании алгебраических выражений установилась практика: при делении числа на произведение, в котором опущены знаки умножения, можно не заключать делитель в скобки, т.е. писать a:bcd
Не кажется ли вам, что вся путаница именно в том, что автор этой задачи использовал алгебраическое правило опускания знака в чисто арифметическом примере и сам вопрос не совсем корректен? Наподобие загадки «сегодня на улице 0 градусов, а завтра в два раза холоднее»
Мне не интересно, что думал автор этой задачи. Когда я решаю задачи, то по умолчанию считаю автора задачи компетентным математиком и он знает правила пропуска знака умножения.
В задаче 6:2×(1+2) = 6:2×3 = 3×3 = 9 нельзя прописанный знак умножения заменить на пропущенный. Потому что, согласно правил пропуска знака умножения, пропускать знак можно только если двойка является множителем по отношению к скобке, а не делителем, как в данной задаче.
Пропустить знак можно, если стоит дополнительная скобка. 6:(2×(1+2)) = 6:(2(1+2)) = 6:2(1+2) = 6:(2×3) = 6:6 = 1 или если мы выносим общий множитель за скобки 6:(2+4) = 6:2(1+2) = 6:(2×3) = 6:6 = 1
Если хотите разобраться в этом вопросе, зайдите по ссылке:
http://www.bolshoyvopros.ru/questions/181097-skolko-budet-621-2.html#answer10731054
Там я под ником KrissVin объясняю, как решается данное алгебраическое числовое выражение.
Дебил, а не инженер
Сами же написали:
Случаи возможного пропуска знака умножения:
1) между буквенными множителями;
2) между числовым и буквенным множителем;
3) между множителем и скобкой;
4) между выражениями в скобках.
1) сразу пропускаем, так как буквенного множителя нет
2) тоже самое
3) То есть между множителем и скобкой, то есть множитель в данной ситуации 6:2, но никак 2 не может рассматриваться как отдельное число, только если бы вместо деления был бы знак минус.
4) между выражениями в скобках, сомнительно, но тоже можно применить (6:2), так как в данном выражении 2 не выступает как что-то отдельное и всю часть примера после знака деления нельзя рассматривать как знаменатель.
«в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления» ну это для меня что-то новенькое…
Для тех, кто прогуливал уроки математики, а на уроках ворон за окном считал это “что-то новенькое…”
Вы неверно раскрыли скобки, так не раскрывают 6:(2×1+2×2)=1Общий множитель можно внести в скобку
А давайте ещё делимое внесём в скобку. (6:2×1+6:2×2)=9
%)
Есть простой пример 6/2(1+2) = 1 или по другому 6/х = 1 В результате х = 6
(во всех примерах 6 в числителе, а 2(1+2) в знаменателе)
Те, кто видит в ответе 9 пусть решат пример 6/х = 9. В результате х = 2/3.
Отлично, значит они считают, что 2(1+2) = 2/3. Пусть докажут это!
Для тех, кто реально работает с формулами 6/2(1+2) = 1
Для жертв ЕГ это 9. Не дай бог им доверить расчет дома, рухнет.
Такой пример решают в начальной школе. Простой способ, представить числа в скобках как «а».
Получаем: 6/2а= 3а
а= 2+1
3а=3*(2+1)=3*3=9
Каким образом Вы превратили 1/2 * (1+2)=3/2 в = 1/6 ?
По вашему 6= 3а×2а? А как с квдратом?
Не дай бог, что бы у делимого отнимали делитель и засовывали его под икс другому множителю. Вот и доказывай потом таким
Для не жертвы ЕГ(Э!) сложно понять, что разные ответы основаны на том, что запись нельзя трактовать однозначно? Даже в примерах выше приведены выдержки из учебника, в которых сами математики до конца не уверены в корректности. Кроме того те кто будет вести «расчет дома» — явно будут знать какой порядок действий должен быть, так как при необходимости они сами будут эту запись составлять.
>>значит они считают, что 2(1+2) = 2/3. Пусть докажут это!
Ничего, что такое равенство получилось сугубо из твоего личного видения ситуации, а конкретно из примера 6/(2*(1+2))? Когда те, кто придерживаются ответа 9, эту запись рассматривают так 6/2*(1+2) ? Или ты предлагаешь бред придуманный тобой доказать?
В вашем примере уравнение должно быть записано так:
(6/х)*(2+1)=1
Отсюда х будет равен 18. А это не так.
Если же решить уравнение (6/х)*(2+1)=9
то х=2 . Что и требовалось доказать.
Для жертв ЕГЭ и для тебя в частности предлагаю воспользоваться гуглом, или учебником по математике для младших классов, где прочитать параграф о порядке арифметических действий )))
Сначала раскрываем скобки, а потом выполняем слева направо все действия умножения и деления.
6/2(1+2) = 6:2*3 = 3*3 = 9
в наше время учили так если между двойкой и скобками знак умножения не ставится то выражение 2(1+2) является одним числом его надо просто упростить ,а вот когда выражение записано 2*(1+2) то здесь два множителя и пример решается по порядку слева. Поэтому в первом выражении 6: 2(1+2)=1 а во втором выражение 6:2*(1+2)=9
Чувак выше пробил дно. Доказать что 1/2*(1+2)=2/3? Сразу видно опытного хумунитария. Или троля который просто выдирает кусок из контекста. Если нужно выражение представить в виде делители без употребления черты то его берут в скобки. Нет скобки — приоритет в порядке очереди.
А кто вам дал право 2(2+1) пихать в знаменатель?
Вот от ваших расчетов дома и рушатся!
Тем кто считает что множитель 2 для (2+1) и 2(2+1) знаменатель (делитель) еще немного арифметических правил:
«…
Знак умножения в некоторых случаях можно опускать, а в некоторых — нельзя:
когда знак умножения принято опускать:
перед скобками:
5·(3+C) = 5(3+C)
перед буквами в буквенном выражении:
5·A·B = 5AB
знак умножения всегда ставят перед числом:
5A = A·5
Свойства умножения:
Переместительное свойство — от перестановки местами множителей произведение не изменяется:
А·B = В·А
…»
А теперь смотрим:
6:2(2+1)=6:(2+1)*2 (обана! умножение вернулось) = 6:3*2 =4
еще один ответ в копилку?!? 🙂 Те кто получает ответ 1 нарушает Переместительное свойство умножения! и в выражении у нас знак деления, а не дробная черта разные вещи по сути, знак деления можно заменить дробной чертой но только правильно!
А если множитель 6:2 (а почему нет?), то все правила соблюдаются!
6:2(2+1)=(6:2)(2+1) (разве мы не имеем права ставить скобки не нарушая правил? Возьмем множитель в скобки! Причем знака умножения до сих пор нет) = (6:2)*3 (помним что перед числом всегда знак умножения) = 3*3=9
и мы не нарушаем Переместительного свойства: (6:2)(2+1)=(2+1)(6:2)=3*3=9
Все еще считаем 2 множителем для (2+1) и 2(2+1) знаменателем?
“немного арифметических правил”
Пропуск знака умножения – правило алгебраическое. Поэтому забудьте арифметику.
“когда знак умножения принято опускать: перед скобками: 5•(3+C) = 5(3+C)”
Не перед скобками, а между МНОЖИТЕЛЕМ и скобкой. Двойка МНОЖИТЕЛЬ по отношению к скобке и при любой конфигурации математического выражения, множитель 2 должен быть умножен на скобку.
Множитель не 2, а 6/2. Какого хрена вы разрываете выражение в удобном вам месте? И вообще, как вы решите, например, такое 6/2(1+2)(2+3) ?
Согласен, напоминает 2(1+2) как будто (1+2)(1+2) то есть 6÷3×3 что ли??? Так здесь и третий вариант ответа 🙂
2(1+2)=(1+2)+(1+2)=6 , 6÷6=1, а Вы неправильно решили 2(1+2)не=(1+2)(1+2)=(1+2)^2=3^2=9
Веселюсь уже второй день! как-то раньше не натыкалась на этот прикол. самое удивительное, что все так близко к сердцу приняли этот софизм. вот интересно, откуда у него ноги растут? кто-то же «нарисовал» такое чудо?
друзья! эту «проблему» не решить в отрыве от контекста. каков источник возникновения данного выражения?
если это арифметическое выражение (ну там, например, по задаче), то оно ЗАПИСАНО НЕВЕРНО. так как при выполнении АРИФМЕТИЧЕСКИХ операций необходимо записывать ЗНАКИ действий. и если «восстановить» знак умножения, то это 9 (к счастью предложения Александрова и Колмогорова не встретили поддержки). то есть уточняю: при выполнении арифметических операций с числами у умножения нет преимуществ перед делением.
а вот если рассматривать это прикольное выражение само по себе, как есть, то отсутствие знака умножения говорит о том, что мы имеем дело не с числами, а с одночленами (если что, то число является частным случаем одночлена). и тогда действительно, двойка относится к сумме. и делить 6 надо на результат умножения, то есть ответ 1.
преклоняюсь перед автором этого софизма. такой хайп запустил!
Прочитайте вслух выражение 8:2а
(Это для тех, кто не понял)
Восемь делить на два и умножить на а. Прочитал, что дальше?
Неверно. Во-первых, арифметическое выражение — это частный случай алгебраического. Поэтому если предложение не поддержано для арифметики, то оно не поддержано для всей алгебры. Во-вторых, в данном случае произведение одночлена и многочлена, а в алгебре _встречается_ (но не всеми математиками признается) исключение из обычного порядка вычисления выражений только для одночленов без знака умножения.
А поскольку здесь произведение на многочлен, то это исключение сюда ни за какие уши не притянуть.
А не легче просто проверить таким способом.
a/2(1+2)=6
a/6=6
a=6*6
a=36 что даёт нам не правильный ответ
А если :
a/2(1+2)=1
a/6=1
a=1*6
a=6 а так вдруг все сошлось)
Вообще задача стояла так ,6÷2(1+3) не пойму что вы обсуждаете,
Знак деления — математический символ в виде двоеточия (:), обелюса (÷) или косой черты (/), используемый для обозначения оператора деления.
Основная функция скобок – менять порядок действий при вычислениях значений числовых выражений. Например, в числовом( арифметическом )
выражении это
5*3+7 сначала будет вычисляться умножение, а потом сложение:
5⋅3+7=15+7=22
А вот в выражении 5⋅(3+7) сначала будет вычислено сложение в скобке, и лишь потом умножение: 5⋅(3+7)=5⋅10=50.
Однако если мы имеем дело с алгебраическим выражением, содержащим переменную — например таким:
2(x−3)
– то вычислить значение в скобке не получается, мешает переменная. Поэтому в таком случае скобки «раскрывают», используя для этого соответствующие правила.
Поэтому в данном случае 6 :2(1+2) это арифметика епта и поэтому сначала считаются скобки т.е 1+2 =3 6:2=3 и 3*3=9
а то что вы написали, даже если поставить дробь вместо деления т.е. правильно
6/2*(1+2)=3*3 или 18/2 как угодно 9. И не путайте алгебраическое выражение с неизвестными где число возле скобок без умножения и скобки воспринимаются как единое целое с арифметикой.
И все споры тут ниочем , считать 2(1+2) единым целым или нет , нет не считать. А считать только если 2(1а+2b).
И 6:2*(1+2)=9 это тоже уравнение только без неизвестных!
Не все верно. В алгебре исключение из общего для всей математики порядка вычисления выражений встречается (причем не у всех математиков) только для одночленов без знака умножения. Произведение числа и суммы чисел, — это произведение одночлена и многочлена. Исключение для одночленов без знака умножения сюда никак не пристегнуть.
Наконец-то. К вашим словам могу ещё добавить одну логическую заметку: 6:2(1+2). После выполнения действия в скобках вы просто уже вынуждены будете поставить пропущенный знак умножения. Или же мы получим такое вот выражение: 6:23. То есть нужно вставить знак между 2и 3. Иначе 23
Пример очень нашумевший, конечно!.. Сейчас в уже в соц сетях обсуждают по полной!:)).
Рассуждая о правильном ответе в математическом выражении 6:2(1+2), нужно применять основы математической методологии!
Возьмем два примера 6:2(1+2) и 6:2*(1+2). В этих выражениях в правой части после знака деления мы видим два отличающихся визуально действия 2(1+2) и 2*(1+2). В чем здесь принципиальная разница помимо того, что мы видим визуально??? В выражении 2*(1+2) мы видим два параметра 2 и (1+2), разделенные знаком «умножение». Эти два параметра независимы друг от друга! То есть, посчитав выражение в скобках, общее выражение можно написать в виде — 2*3. То есть оно тождественно 2* (1+2). Говоря методологически — мы не обязаны после совершенных действий в скобках сразу умножать результат на 2. То есть 2*(1+2)=2*3. Эти элементы (параметры) 2 и (1+2) могут взаимодействовать друг с другом посредством какой-то математической операции, в данном случае «умножение» (*). Но при этом они друг от друга не зависимы!!!!. Так как они могут быть записаны в пределах одного выражения разными способами, они обособлены и имеют полноценное право на взаимодействие с любыми элементами в пределах каких-либо правил математического взаимодействия. То есть подставив выражение 2*(1+2) в выражение 6:2*(1+2), оно начинает «подчиняться» вновь появившимся правилам взаимодействия! После действий в скобках начинается деления 6 на 2, и только потом умножение на результат в скобках. То есть срабатывает «независимость» 2-йки от других элементов выражения, и дальнейшие действий подчиняются базовым законам исчисления!. Значит ответ в данном случае — 9.
А теперь посмотрим на выражение 2(1+2) . В чем принципиальное отличие от предыдущего примера!!?? Отличие практически фундаментально!! В отсутствии знака «умножение» цифра 2 перед скобкой превращается в коэффициент, который может иметь как усиливающий эффект так и понижающий. То есть 2-ка имеет прямое влияние на скобку!!!. Выражение в скобках уже априори «усилено» 2-кой перед скобкой!!!!!!!!!. Результат выражения в скобках АВТОМАТИЧЕСКИ ( в данном случае) «усиливается» в 2 раза!!! То есть, как только мы посчитали (1+2), то оно сразу превращается в 6-ку!!!!!!! Выражение 2(1+2) едино, оно не зависимо от других выражений. Все действия в рамках этого выражения имеют приоритет перед другими действиями в более широких арифметических пределах! То есть, подставив выражение 2(1+2) в выражение 6:2(1+2) — мы получаем 6:6=1!!!!!!! И ни как иначе!!!!!
___________________________________
выводы:
1. Если в условии задачи стоит пометка типа «выполните простое арифметическое действие..», либо явно стоит знак «умножение» — то считать нужно по правилу «слева на право». То есть ответ будет 9.
2. Если нет ни каких пометок и комментариев и нет знака «умножение», то считать нужно по второму принципу, и ответ будет 1. Как говорил один мудрый профессор: — С(А+В) и С*(А+В) — это разные вещи!!
3. Ставьте дополнительные скобки для подстраховки!:).
P.s. «Правильная» постановка задачи ведет к «нужному» решению!:))
Всем удачи!!
Я выше постарался ответить на «Никак иначе». Еще «иначе» получилось. По согласно переместительному свойству умножения: 2(2+1)=(2+1)*2 (перед числом ВСЕГДА ставится знак умножения). А теперь подставьте в исходный пример и посмотрите что вышло.
Если вы ставите знак умножения, то должны написать скобки 6:2(2+1) = 6:((2+1)×2) = 6:(3×2) = 6:6 = 1.
Цитата из Методики преподавания алгебры в восьмилетней школе Репьева В. В., стр. 81:
«Если бы в делителе были записаны знаки умножения, то пришлось бы написать:
a : (b×c×d).
… при делении числа на произведение, в котором опущены знаки умножения, можно не заключать делитель в скобки, т.е. писать:
a : bcd.»
https://russianclassicalschool.ru/biblio/11_sr_sk_metod_algebra.pdf
Откройте хотя бы онлайн калькулятор от Гугл. Введите выражение без знака умножения и посмотрите на ответ. Удивительно, но ответ = 9.
Возможно, Гугл и его команда не знает Ваше правило про «усиление» в случае отсутствия знака умножения, а также не знает изречение «мудрого профессора».
Вот и считает буржуйский сервис неправильно.
А помимо гугла еще сотня онлайн инженерных калькуляторов не знают правила «усиления», и тоже выдают ответ 9ку. Безграмотные, что тут сказать.
чтож давайте мерятся буржуазными калькуляторами 🙂
давайте возьмем инженерный калькулятор из Виндовс10.
Он даже не позволяет ввести выражение вида 6:2(2+1) так как оно может иметь разночтение и поэтому он считает такое выражение недопустимым.
Итак кто круче? Гугл или Мелкософт? Ларри или Билли? :)))
получается: 8:(1+1)(2+2)=1 ?
В данном случаи, получается, что 6:(1+1)(1+2)=1? Ведь 6:2(1+2)=6:(1+1)(1+2). Странно как-то.
П.1 Вещь одна, но используется по-разному. 9-)
Автор высосал рассуждение из ничего, при том, что сам и дал ответ:
3) между множителем и скобкой;
Ответ тут 1 и нехрен спорить. Хотя, конечно, автор прав и следует избегать таких записей, которые вводят в заблуждение «инженеров» 🙂
Но математика — точная наука.
У нас нет такой операции «пусто», она нигде не вводится и нигде не определяется как полный аналог операции умножения (да это и бессмысленно).
У нас определяется лишь возможность упрощение записи выражения в четырех описанных случаях, когда операцию умножения можно опустить.
И опуская операцию умножения мы семантически превращаем такое выражение в единое целое, которое, соответственно, должно вычисляться до применения каких-либо операций с ним.
Я думаю, что ответ прост — 9.
Контраргументы достаточно сомнительны из теории «а мне так думается».
А проверка до боли простоя — откройте десяток российских инженерных калькуляторов онлайн, а затем десяток зарубежных.
Вбейте туда этот пример точно в таком же виде, как он записан
6:2(2+1)
Обращаю внимание — знак деления в виде двоеточия или обелюса, НЕ косая черта; знака умножения перед скобками нет.
Для экономии Вашего времени — из 20 калькуляторов 20 показали ответ 9.
Думается мне, что все-таки это единственно верный ответ.
Конечно, есть и такие, кто скажет (знаю таких лично) — это все ерунда, эти калькуляторы считают неверно. С такими людьми спорить бессмысленно, для них и черное будет белым
Между множителем и скобкой. Я не эксперт. Но там не сказано, что это обязательно должен быть чистый множитель ДЛЯ скобки. Поэтому мне кажется, что ничего не меняется с этим правилом. Ответ остаётся тем же. 9. Ведь пример всё ещё спокойно сводится к 6÷2*3.
какой интересный у вас множитель 6÷2)) тогда уж сразу 3*3. но это нас не устраивает потому что есть формула и в ней есть множитель (уже есть) поскольку знак уже упущен и он = 2 и должен быть умножен в любом случае на то что получится в скобках, ведь он их множитель)
а давайте посмотрим на это вот так:
6:2с
пусть с=2+1 тогда 6:2с=1
теперь просто подставим значение в изначальный пример и выходит 6:2(2+1)
так все же сколько? :)))
Калькулятор Panecal, ответ 1
мне попалась вот такая книга: Методика преподавания алгебры, Курс лекций, Шустеф М. Ф., 1967 г.
там на 48 странице есть вот такая информация:
Порядок действий. В алгебре тот же порядок действий, что и в арифметике, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например a:b*c=a:(b*c).
Давайте посчитаем с учетом новых знаний 🙂
Это не «исключение», а полная замена порядка вычисления выражений на вычисление умножения строго раньше деления. А поскольку арифметическое выражение — это частный случай алгебраического, то этим Шустеф утверждает, что общеизвестный и общепринятый порядок вычисления выражений отменяется и заменяется на указанный им. Чего, как известно, не произошло.
Шустеф просто замастерился. 🙂
В арифметике мы стараемся найти решение только одного данного вопроса с известными определенными числами.
В алгебре — найти общее решение всех вопросов одного рода, какие бы числа не были даны. Алгебра имеет дело не с числами, а с буквами, которые могут обозначать какие угодно числа.
Раскрытие скобок по правилу 2(а+b)=2a+2b является алгебраическим правилом. Любые другие правила и примеры с переменными, которые приводят выше, также являются алгебраическими.
Т.к. в нашем примере 6:2(2+1) нет переменных и все числа известны, то применяются арифметические правила. Следовательно, вначале действие в скобках, а затем по порядку слева направо.
6:2(2+1)=6:2*3=3*3=9
Доп скобок нет. Так что в дробном виде…
6 (2+1)
—- X ———- = 6
2 1
6/2(2+1)=6(2+1)/2=9
Всё правильно, правильный ответ 1
Знак умножения опускают не для того, чтобы поменять приоритет. Никогда такого не было!!! Как победитель городских олимпиад по математике в старших классах говорю))) Знак умножения опускают просто потому, что его можно не писать. Например, как умножение или деление на 1. Написан знак умножения или нет — математический смысл не меняется. И приоритет тоже.
Поэтому эти записи тождественны 6/2(1+2) = 6:2*(1+2).
Ответ 9.
Так было, есть и будет. Либо надо ставить скобки для изменения порядка расчетов, либо горизонтальную черту дроби, которая заменяет скобки. Косая черта — это просто знак деления. Она не может быть заменой горизонтальной черте дроби, т.к. в знаменатель пойдет только первое число или буква или скобка после косой черты.
Посчитайте 500/5(7+3)(4+6)(1+9).
Получите тысячу, сто тысяч или одну десятую???
Не может быть разных ответов в зависимости от убеждений математика.
500/5аbс = 500:5*а*b*с.
А подобные изыски о приоритете умножения, если знак умножения опущен — это современная выдумка. Думаю для того, чтобы наших детей сделать безграмотными. Мосты, рассчитанные и построенные такими вот «инженерами», будут падать от первого штормового ветра.
Как победитель республиканских и участник Всесоюзных олимпиад по математике, рекомендую Вам решить для начала пример из задачника:
10(a+b)³:2(a+b)
Ответ: 5(a+b)²
Что касается примера 6:2(1+2), который Вы не можете правильно решить, информирую Вас — это не арифметический пример! Пропуск знака умножения – правило алгебраическое. Это алгебраическое числовое выражение, которое должно решаться по алгебраическим правилам с учетом правил пропуска знака умножения.
Господа давайте выполним проверку. Возьмем за х любую константу исходного выражения, например 6:
Х:2(1+2) =9
Х=9*2(1+2) =54, но явно не 6
Второй вариант:
Х:2(1+2) =1
Х=1*2(1+2) =6, чтд( что и требовалось доказать). Верный ответ 1, так как ответ 9 не дает верного равенства.
А может вы не поменяли при переносе знак у множителя (1+2)?
х:2(1+2)=9
х=9*2:(1+2)= 6
Что и требовалось доказать!
Вот от таких инженеров — победителей олимпиад и мосты рушатся. и дома валятся. и самолеты падают…Это новое слово в математике!!! Горизонтальная черта дроби это и есть знак деления.( хоть косая, хоть двоеточие!)
А проверить не пробовала? Замени любую константу на «Х» , подставь в выражение и проверь для случая с ответом «1», и с ответом «9»
Реши и получишь «1»
Читай учебники: Ларичев » Сборник задач по алгебре» 6 — 7 класс.
Шустеф М.Ф 1967 г.» Методика преподавания алгебры»
Лифшиц. Ландау «Курс физики….»
Или они не авторитет?
В вашем примере 6/2а переменная «а» привязана к множителю «2» ЖЕЛЕЗНЫМИ узами и находится она, следовательно, в знаменателе! Т.о. 6/2а=3/а, т.к. числитель и знаменатель мы сократили на 2. Теперь вместо «а» подставляем её значение, а именно: (2+1) и получаем в итоге: 3/(2+1)=3/3=1. Число 2 перед скобкой в выражении 6/2(2+1) является МНОЖИТЕЛЕМ для выражения в скобках; именно на это указывает ОПУЩЕНИЕ знака умножения. Если мы хотим восстановить этот знак, то должны восстановить и «опущенные» скобки, т.е. 6/2(2+1)=6/(2*(2+1))=1. И выражение 6/2(2+1) не идентично выражению 6/2*(2+1) !!!
На каком основании?????
Опускать знак умножения можно ВСЕГДА, если это не создает возможности неправильного прочтения! То есть C*O*S = cos нельзя, C*L*M = CLM — допускается!
6/2(2+1)
Сначала скобки: 6/2(3)
Потом слева направо 3(3)
Ответ 9 все остальное от лукавого
Не думаю что кто-то увидит, но я объясню как это понял я:
12:3(4×2)×8:2=?
Если между множителем и скобкой знак убран правильно то 3(4×2) это один множитель, а если нет, то 3×(4×2), то есть (4×2) это отдельный множитель.
Это можно проверить так:
3(4×2) = 3×4+3×2
3×8=12+6, значит (4×2) это отдельный множитель.
24 не равно 18 значит должно быть × между скобкой и 3 следовательно пример равен 128.
Вот ещё пример — 6:2(1+2) =?
2(1+2) = 2*1+2*2
2*3 =2+4
6=6, значит 2 просто вынесли за скобки.
Тогда знака × между скобками нету и 2(1+2) это один член уравнения следовательно пример равен 1.
Читаю комменты и испытываю испанский стыд. Для тех кто прогуливал школу дублирую один из самых первых комментов ещё за далёкий 2013-й год. «Вообще-то со времён школы выполняются сначала действия в скобках, затем умножения и деления слева направо поочерёдно, затем сложения и вычитания слева направо поочерёдно. Пропущен знак умножения или нет — неважно, важно, что он понятен и присутствует. Деление (двоеточие) не то же самое, что дробная черта. Данное выражение можно было написать и как 6:2х3»
Для совсем «Иванов» есть в природе инженерные калькуляторы, они как ни кто лучше всех вас вместе взятых знают как надо решать данное уравнение и в какой последовательности проводить те или иные манипуляции. У кого нет такой приблуды на руках, могут запустить кальк у себя на винде и перевести в режим инженерного. Проверить его можно такой же приблудой в онлайне от гугла — в интернете же вас ещё не забанили. Смотрим на результат, радуемся и искренне проклинаем Била Гейтса, Ларри Пейджа и Сергея Брина.
Рассуждения о сферическом коне в вакууме бессмысленны. Если в решебнике ответ «1» — значит нужно читать условия на данное задание (автор его не предоставил). В нашем же случае дано сухое уравнение без всяких прочих, как следствие это имеет значение (!). Во всех остальных случаях (без доп. условий) пользуемся общеизвестными правилами (решаем скобки и проводим поочерёдные действия слева направо). Всё, и никаких скрытых смыслов, просто простые правила.
Фраза от автора данного поста просто повергла в шок «От себя скажу, что я часть после деления воспринимаю как нечто целое, т.е. скобку с множителем, мне это кажется вполне естественным.» Ему мля кажется, вы понимаете, ему кажется… Facepalm… Есть правила, и ничего казаться не будет. А сама фраза звучит как «немножко беременна».
А все горящие жопы и недовольные единственно правильным ответом «9» — добро пожаловать на второй год школьного курса математики 4-го класса, туда вам самая дорога.
Boshetoonmay
6:2(1+2) = 6:(2×3) = 6:6 = 1
А «всем горящим жопам», у которых понимание математики зависло на уровне арифметики 4-го класса. Кто вместо того, чтобы развиваться дальше и учить алгебру, ворон за окнами считал. «Добро пожаловать на второй год школьного курса математики 6-го класса».
Пример 6:2(1+2) не арифметический и в 4-м классе Вас не научат его решать. Пропуск знака умножения — правило алгебраическое. Соответственно 6:2(1+2) это алгебраическое числовое выражение, которое должно решаться по алгебраическим правилам с учетом правил пропуска знака умножения.
Вооружайтесь математической литературой для 6-го класса и начинайте изучать. Успехов Вам.
Методика преподавания алгебры, Репьев В. В. (стр. 80-81)
Методика преподавания алгебры, Шустеф М. Ф. (стр. 43)
Методика преподавания математики в восьмилетней школе Ляпин С. Е. (стр. 359, 363)
Методике преподавания алгебры Барыбин К. С. (стр. 139, 184)
Построй свою математику. Блок тетрадь эталонов для 5 класса. Петерсон Л. Г. Москва 2007.
Что же касается калькуляторов, то для того чтобы получить правильный ответ, необходимо пользоваться калькулятором в инструкции/описании которого есть знак «Умножение, где знак умножения опущен». Иначе нет гарантии правильного решения. Если же в инструкции/описании есть знак «Умножение, где знак умножения опущен», то он по приоритету стоит выше деления. Прилагаю инструкцию, смотрите страницу R-8.
https://support.casio.com/ru/manual/004/fx-82_85_350ES_PLUS_RU.pdf
«Для совсем “Иванов”» рекомендую «запустить кальк у себя на винде и перевести в режим инженерного». Вы убедитесь, что при попытке ввести пример с пропущенным знаком, у Вас это не получится. И в Excel тоже, выдаст ошибку.
Я постарался выдержать Ваш стиль общения и кое-что даже цитирую из Вашего опуса. Вы пишете, что «испытываете испанский стыд», а у меня осталось чувство, что с гопником общаюсь.
Репьев — утверждает что в алгебре установилась практика при делении числа на произведение, в котором опущены знаки умножения, не заключать это произведение в скобки, т.е. писать a:bcd. Это, мол, ограничивает правило последовательности вычисления выражений и составляет исключение из него. Но в качестве примера приводится деление только на одночлен в стандартной форме, что действительно составляет достаточно общеизвестное исключение из этого правила. Однако он не привел более общего случая — деления числа на произведение, в котором участвует многочлен. Очевидно, что этот вариант не пришел ему в голову, так как если бы он действительно распространял свою формулировку и на такие выражения, логично было бы привести пример, исключающий любое недоразумение, порождаемое последовательностью вычисления выражений (но это уничтожило бы опциональность опускания знака умножения, а его все описывают именно как опциональное, а не способ записи неразрывных произведений).
Шустеф: «В алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается». В качестве примера приводит уже более однозначное и неверное равенство a:b*c=a:(b*c), впрямую нарушающее последовательность вычисления выражений. При этом отмечает, что два математика предлагали вообще отдать умножению более высокий приоритет перед делением, но это предложение не нашло поддержки. Между тем, арифметическое выражение является частным случаем алгебраического, поэтому утверждение Шустефа все-таки означало бы именно изменение порядка вычисления выражений, включающих умножение и деление. Кроме того, он перепутал причину со следствием. Алгебраические одночлены без знака умножения связаны сильнее, поэтому такая запись и используется, когда надо обозначить эту связность. А опускание знака умножения, когда это возможно, везде называется опциональным, а не способом связывания сомножителей.
Ляпин — просто использует неразрывность одночленов без знака умножения. Это известное исключение из порядка вычисления выражений, его многие если не большинство не оспаривают. Произведения с участием многочленов в качестве делителя он в своих примерах не приводит, поэтому к нашему случаю отношения не имеет.
У Барыбкина на с. 139 речь идет только о делении на одночлен, в то время как у нас произведение одночлена и многочлена, на 184-й — речь о дробях и тоже используется уже известная нам неделимость (или если угодно «более сильная связь») одночленов без знака умножения. Не наш случай.
Петерсон — изделие не является общедоступным, следовало привести фотографию.
А по ссылке https://dzen.ru/a/YEy2pGyGHwEHMhIZ приведен пример учебника, в котором, по утверждению автора, имеется решение примера 27:3(11-8) = 27:3×3 = 9×3 = 27, и пособие «Алгебра для самообразования», в котором все одночлены после знака деления берутся в скобки (возможно впрочем просто во избежание недоразумений). (Третий пример там мне показался не убедительным).
Для всех у кого получилось 1.
https://www.youtube.com/watch?v=ZRRlw3WkMB0
Для всех у кого получилось не 1 -> https://easy-math.ru/solution-viral-school-tasks/
Там ровно то же неверное рассуждение что и здесь. В нем упускается из виду, что множитель должен стоять не только перед опущенным, но и присутствующим знаком умножения. Это не делает незаконным выражение 6:2*(2+1) или равное ему 6:2*3, которые вычисляются по всем известным с третьего класса правилам. То же относится и к тому же выражению с опущенным знаком умножения.
Ребята, если у вас что то вызывает подозрение, вы всегда начинаете делать невзирая на сомнения? Не проверяете никак?
А ведь до того, как мы начнем считать, чему равно это выражекние, мы имеем право и обязаны произвести несколько проверочных действий. Или, если хотите, привести выражение к удобному виду.
1. Применив переместительный закон математики 6:2(2+1) = 6:(2+1)2= (должно быть одинаково) Поменяли местами сомножители
2. Применив распределительный закон математики 6:2(2+1) = 6:(4+2) = (должно быть одинаково) Внесли сомножитель в скобки.
3. Применив сократительный закон (сократили одинаковые сомножители. Представив 6 как 2х3 Получим 6:2(2+1) = 2х3:2(2+1) = 3:(2+1)= (должно быть одинаково с предыдущими примерами
Во всех 4-х случаях (3 приведенных правила и исходный пример) результат должен быть одинаков.
Меня сильно напрягает, что нынешнее правило слева-направо противоречяит нашей же алгебря и физике, где умножение приоритет нее деления. Хуже того, он противоречит правилам в некоторых других странах.
Я могу предполагать, для чего наших школьников дебилами делают с помощью таких правил. Это аукнется нам чуть позже, когда на международных соревнованиях американцы начнут массово применять такие неоднозначные примероы.
О себе, 65 лет, победитель всех школьных и районных олимпиад 1969-1974. Неоднократный призер краевых олимпиад по математике.
Во всех трех «проверках» вы сразу исходите из предположения, что множителем при скобке (2+1) является 2, а не 6:2, то есть подсовываете доказываемое в качестве посылки. 🙂
А то, что этим множителем является 6:2, задается последовательностью вычисления выражений, которая проходится в третьем классе.
То есть, 1) 6:2(2+1)=(2+1)6:2=9 ; 2) 6:2(2+1)=6:2х2+6:2х1=6+3=9 ; 3) 6:2(2+1) = 2х3:2(2+1) = 3(2+1)=9 . Но это тоже не проверки, а просто разные способы вычисления одного и того же, исходя из исходно выбранного понимания исходного выражения.
Умножение не приоритетнее деления. В других странах эта же последовательность вычислений обозначается PEMDAS (по первым буквам действий). Просто в алгебре не принято разрывать делением одночлены в стандартном виде (или близком), состоящие из произведения числа и переменных без указания знака умножения. Они в любом случае отличаются от любых других алгебраических выражений тем, что в них нельзя подставить числовые значения переменных.
Но некоторые методисты и на такие выражения распространяют стандартную последовательность вычисления выражений. Думаю что зря.
Во всех остальных случаях опускание знака умножения является опциональным, а это значит что опущенный знак умножения подчиняется последовательности вычисления выражений точно так же как и указанный в явном виде.
А олимпиады вы при таких представлениях выигрывали потому, что в наше время все писалось от руки, и в качестве знака деления практически всегда использовалась горизонтальная черта, с которой все всегда однозначно. Сегодня пытался продемонстрировать коллеге неразрывность выражений типа 2abc по справочнику Корна и Корна, — и не нашел там подходящих примеров, — везде только горизонтальная черта. 🙂
2(1+2)=(1+2)+(1+2)=6 , 6÷6=1, а Вы неправильно решили 2(1+2)не=(1+2)(1+2)=(1+2)^2=3^2=9
За эти года уже можно было например и у Григория Перельмана спросить за этот пример.
6:2(1+2) опущеный знак умножения, это алгебра. Данное выражение необходимо преоброзовать в математическое, чтобы появился опущеный знак умножения. Для этого используется правило переноса множителя за скобки, но при этом сохраняем условия задачи по алгебре. Таким образом появляются вторые скобки.
6:2(1+2) = 6:((1+2)×2) = 1
( 9? ) вам уже всё разжевали и в рот положили, но и этого мало, ещё пенка надо дать под зад, чтобы проглотили. ЕГЭ это позор, оно делает из людей баранов.
Арифметическое выражение — это частный случай алгебраического. А при опускании знака умножения не оговаривается, в алгебраическом выражении это происходит или арифметическом.
Если знак умножения можно, а не надо было упустить, то его можно и вернуть. В любом случае, опущен он был в выражении 6:2*(1+2), а это задача на последовательность вычислений для третьего класса с ответом 9.
А «разжевали» ерунду. Знак умножения не только опускается, но и стоит перед множителем, — это не делает в выражении 6:2*(1+2) множителем число 2. Это просто означает, что таким множителем как в этом выражении, так и в равном ему 6:2(1+2) является выражение 6:2.
Я имел в виду не «перед множителем», а «после множителя», — оговорился..
6:2(2+1)=?
Раскрывать скобки также следует по порядку. — если перед скобкой стоит плюс — знаки оставить — если перед скобкой стоит минус — знаки поменять — если перед/после скобки стоит множитель — умножить каждое число в скобке — если после скобки стоит делитель — разделить каждое число в скобке.
Согласно этому вывод решения данной задачи следует,
6:2(2+1)=>
2(2+1)=>4+2=>6
6:6=1
Дети эту задачу решили на палочках.
Я даю им калькулятор и предлогаю представить доказательства физически своему решению.
В математике теорема — это утверждение, которое было доказано на основе ранее установленных утверждений: других теорем и общепринятых утверждений, аксиом. Теорема является логическим следствием аксиом. Доказательство математической теоремы является логическим аргументом для утверждения теоремы, приведенного в соответствии с правилами формальной системы. Доказательство теоремы часто интерпретируется как обоснование истинности утверждения теоремы. В свете требования, чтобы теоремы были доказаны, концепция теоремы является принципиально дедуктивной, в отличие от понятия научного закона, который является экспериментальным.
Нет оснований утверждать, что множителем в данном случае является 2, а не 6:2, как и в случае 6:2*(2+1) — эти выражения в этом смысле полностью эквивалентны. Но существует общеизвестный и общепринятый порядок вычисления выражений со скобками. Сначала вычисляются скобки (6:2*3), потом выполняются операции умножения и деления слева направо (3*3=9), потом — сложения и вычитания слева направо (здесь таких не осталось).
Все остальное — выдумки интерпретаторов.
Если кому то необходимо получить ответ (9) запишите пример в таком виде: (6:2)(1+2)= 9 Между скобками , как раз, знак умножения можно не писать ! Сразу пропадают все разногласия ! Что если 6: (1+2) = 2 Но всем известно что скобку можно представить в виде 6 : 1*(1+2)= ? Вроде абсолютно ничего не изменилось, но теперь если выполнять действия по порядку, мы должны число 6 не делить на скобку, а умножать !!! И ответ будет равен 18 !!! Граждане, включите мозги, разве можно общий множитель отрывать от его скобки ?!!!
Мне кажется тут все проще. Нужно разделить 6 яблок на 2 группы по 1+2 человека (2 взрослых и 1 ребенок). У кого получилось 9, считайте себя Иисусом Христом, накормившим 5ю хлебами тысячу человек.
«Мне кажется тут все проще. Нужно разделить 6 яблок на 2 группы по 1+2 человека (2 взрослых и 1 ребенок). У кого получилось 9, считайте себя Иисусом Христом, накормившим 5ю хлебами тысячу человек.»
Все еще проще. У прапора 6 танков в ангаре, на половине из них должно стоять две рации и тепловизор. У кого при этом в документах посчитан только один прибор — тот себе новую машину скоро купит.
Если знак умножения может, — а не должен, — быть опущен, то его можно было и не опускать. Поэтому независимо от того, кто что думает о допустимости или недопустимости обратной операции, выражение, в котором знак был опущен, исходно выглядело так:
6:2*(1+2)
А это задачка на последовательность вычисления выражения для третьего класса, ответ в которой однозначно 9.
В чем ошибка автора исходной публикации? Он упустил из виду, что множитель при операции умножения может определяться предшествующими вычислениями. Именно это мы и имеем в обеих эквивалентных записях. Знак умножения тоже ставится только между множителями. Между делителем и множителем его ставить нельзя. Но это означает просто, что первым множителем здесь является выражение 6:2. Брать его в скобки нет необходимости, потому что это задается последовательностью вычисления выражений.
В математике есть два бесспорных обстоятельства, которые никто не станет отрицать: последовательность вычисления выражений (скобки->умножение и деление слева направо->сложение и вычитание слева направо) и возможность опустить знак умножения везде, где это не меняет смысла выражения (например, между двумя числами — нельзя). Если мы позволяем пропуску знака умножения менять последовательность вычисления выражения, то этим отменяем необязательность его опускания во всех случаях, где это повлияет на порядок вычисления выражения.
Есть методисты, которые абсолютизируют это и распространяют общепринятую последовательность вычисления даже на выражения типа a:bcd (трактуют их как а:b*cd). А в пособии «Алгебра для самообразования» Д.К.Фаддеева и И.С.Соминского 1996-го года авторы стабильно берут одночлены без знака умножения в скобки, если они стоят после знака деления (например, bc:(3bcd) ). Возможно, впрочем, это просто для однозначности.
Но такие выражения являются достаточно естественными исключениями из последовательности вычисления выражений. Во всей остальной алгебре, кроме таких выражений, мы можем подставить вместо переменных их значения, ничего больше не меняя. Но в выражениях типа 2ab, cde и пр. мы не можем этого сделать, не вставив между переменными знак умножения. Это дает нам основания рассматривать такие выражения как «исходно такие». В любом случае, это особые чисто алгебраические сущности. Так почему бы заодно, просто для удобства, не считать, что они стоят в невидимых скобках?
У нас нет никаких оснований распространять это на более сложные выражения, получаемые за счет опускания знака умножения, типа 6:2(1+2), потому что тогда это будет уже не опциональным опусканием знака умножения, а записью, меняющей последовательность вычисления выражений, — даже числовых. Кто-нибудь где-нибудь видел уточнение, что опускать знак умножения допускается только когда это не меняет последовательность вычисления выражения? Нет, потому что его пропуск НИКОГДА не меняет эту последовательность.
Читаю этот блог и меня не покидает одна мысль — как мало у нас хороших преподавателей математики! Ведь это очевидно, что многие здесь продолжают отстаивать свою точку зрения не потому, что они до сих пор не поняли суть вопроса, а потому, что они не могут смириться с тем, что, оказывается, их так плохо учили, что они не смогли сразу дать правильный ответ, а теперь признать это для них всё равно, что плюнуть на свое отражение в зеркале. Они будут повторять одни и те же доводы только бы последнее слово осталось за ними и создало у кого то впечатление, что они правы…
Кажется в классе шестом к нам пришла новая учительница математики. Она представилась, села за стол и стала нас рассматривать. Потом написала на доске два выражения 2*(1+2) и 2(1+2), опять села за стол и спросила — «Как Вы считаете это взаимозаменяемые выражения или нет?»
Несколько человек сразу ответили, что Да, а некоторые даже с гордостью пояснили, что это так, потому что после выполнения всех действий они дают одно и то же значение. Скажу честно, у меня было такое же мнение, но как будто что-то останавливало меня от того, чтобы его высказать — уж больно очевидным был этот ответ. Подождав немного она сказала — «Ну что же, похоже других мнений нет?» И тут я не вытерпел и поднял руку. Она показала на меня рукой, давая понять, что я могу сказать. Я встал и сказал, что есть другое мнение и что эти выражения НЕ взаимозаменяемы. «И почему же?» — спросила она, а я ответил, что не знаю почему, но если бы они были взаимозаменяемы, то она не задала бы этот вопрос. Учительница недовольно хмыкнула и пробурчала — «Ну что ж, это лучше, чем ничего…»
И вот что она нам поведала.
«Эти выражения НЕ взаимозаменяемы потому, что они были получены разными путями. Первое выражение диктовали так — 2, умножить, скобка открывается, 1, плюс, 2, скобка закрывается, а второе диктовали так — 2, плюс, 4. Затем из второго выражения вынесли общий множитель 2. В результате, разница этих выражений в том, что в первом 2 перед скобками это самостоятельный член, а во втором 2 это общий множитель, вынесенный за скобки (другими словами: 2, во втором случае, это часть выражений в скобках и с ней нельзя производить действия отдельно от членов в скобках). Представленные самостоятельно эти выражения действительно дают одно и то же значение, но при наличии других членов они ведут себя по-разному, т.к. второе меняет существующий в арифметике порядок действий — выполнение умножения и деления слева направо.»
Она добавила перед каждым выражением 6 и знак деления «:»
6:2*(1+2) и 6:2(1+2)
и продолжила.
«В первом выражении, где между 2 и скобкой присутствует знак умножения, 2 это самостоятельный член и это арифметическое выражение. Здесь сохраняется арифметический порядок действий слева на право (т.е. операция в скобках, деление 6 на 2, умножение результата деления на результат в скобках). Во втором выражении 2 это множитель, который был вынесен за скобки и это алгебраическое выражение и в нём порядок действий отличается от того, что принят в арифметике. В этом случае 2 должно быть умножено на содержимое скобок до выполнения операции деления или же опять занесено в скобки до выполнения деления (т.е. операция в скобках, умножение 2 на результат в скобках, деление 6 на результат умножения 2 на содержимое скобок). Как видите, мы получаем два разных результата 9 в первом и 1 во втором. Вы, конечно, можете сказать, что сейчас Вы от меня узнали, как были получены эти выражения, а как же быть если Вы видите такой пример в задачнике или на контрольной — очень просто — для этого во втором случае и был пропущен знак умножения между 2 и скобками, чтобы сказать Вам, что это алгебраическое выражение и 2 это множитель, а не самостоятельный член и он должен быть умножен на скобки до операции деления.»
Шикарная история! Придуманная или реальная? Если реальная, есть ссылка на учительницу? Сейчас реально найти людей, через тех же Одноклассников. Пытаюсь найти начало этой проблемы.
Чтобы разделить число 6 на произведение состоящее из 2х или более множителей.выражение можно записать так 6:аб но никак 6:(аб) а=2 б=1+2.В данном случае умножение является приоритетным перед делением..Простой пример у нас 6 яблок нас трое каждому по два яблока нас увеличилось в двое нам достанется по 1 яблоку.но не по 9 Если бы у нас было арифметическое выражение6:2*(1+2) в данном случае 9
В математике есть правила, они распространяются на алгебру, геометрию, физику и т.д. На основание этих правил программируют технику. Поэтому возьмите инженерный калькулятор и решите этот пример со знаком умножить и без него. И не нужно разводить тут демагогию. Вольномыслие полное
Правило опускания знака умножения в выражениях.
Знак умножения при записи математических выражений можно опустить в таких случаях:
1. между буквенными множителями;
2. между числовым и буквенным множителем;
3. между множителем и скобкой;
4. между выражениями в скобках.
Наш случай 3. В арифметике знаки умножения не опускаются, а значит это алгеброическое выражение и 2(1+2) — многочлен, т.е. целое и отрывать от него члены и решать кому как заблагорассудиться недопустимо. Поэтому, сначала решается многочлен, а затем все остальное по правилам. Правильный ответ «1».
Для наглядности решим простейшую задачку: Человек проехал путь 105 км, причем половину пути на велосипеде за 2 часа, а вторую половину на машине за 1 час. Обратный путь он совершил аналогично, на той же машине и том же велосипеде. Определить среднюю скорость на всем пути 210 км.
Vср. = S:2(t1+t2) или 210:2(2+1).
По версии ЕГЭшников Vср.=210:2*3
=315 км/час, т.е 210/2 а потом умножаем на 3, что является глупостью.
Правильное решение: Vср.= 210:6=35 км/час. (где 6=2(2+1)). Разделять многочлен 2(2+1) математика не допускает, это целое — в данном случае сумма времени. Еще вопросы будут? Если б я решал алгеброические выражения как некоторые жертвы ЕГЭ, то давно сидел бы в тюрьме, т.к. последствия для меня были бы катастрофические.
Справедливости ради эту задачку можно решить и арифметически: Vср.=210:(2*(2+1))=35 км/час. Только выглядит более громоздко. Разговаривать с теми, у кого получилось 9 в заданном примере, нет никакого смысла, пока они не поймут разницу: 2а — это 1 литр, 2*а — это два по пол-литра. А кто смотрит на калькулятор — значит, что мозгов у него точно не больше чем в калькуляторе. Для калькулятора надо составлять алгоритм решения (правда не для всех, математический Simens решает правильно).
Неправда Ваша ,батенька ,из условия задачи задачи следует: скорость машины Vм=105/2= 52,5км/ч ,скорость велосипеда Vв= 105/4=26.25 км/ч
отсюда средняя Vср=(Vм+Vв)/2=39,375 км/ч. Видно пора Вам в тюрьму.
Средняя скорость так не определятся. Средняя скорость это расстояние, поделенное на время, за которое оно было пройдено. Это определение средней скорости. Поинтересуйтесь.
Здесь речь не о средней скорости машиновелосипеда, а о средней скорости движения человека, который на них ехал.
Коэффициент первичен. Ответ 1. Действия в скобках, потом умножение на коэффициент. И только так. Это одно число 2(1+2). Воспринимать его следует как единый целый объект. А уже потом вокруг есть какие-то другие операнды. Вот если там явно укажут знак умножить, а именно: 2х(1+2) тогда будет 9, и будет порядок действий из 3-го класса общеобразовательной школы. А так ответ 1. Как записано, такой и ответ. И не надо ничего додумывать про умножить, его там не написали. Коэффициент первичен.
реально, естественно, в соответствие установленных правил: 1
Средняя скорость так не определятся. Средняя скорость это расстояние, поделенное на время, за которое оно было пройдено. Это определение средней скорости. Поинтересуйтесь.