Всем привет. Сегодня разберёмся с одной задачей, которая как-то реально встала передо мной на работе. Тогда, правда, всё в маткаде считал 🙂
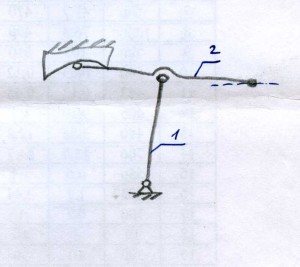
Чтобы показать суть механизма, набросал простую кинематическую схему:
Коромысло 1 совершает небольшие колебательные движения относительно вертикального положения (10-30 градусов). Левый конец шатуна 2 двигается по определённой траектории, которую и нужно найти. Обязательное условие в том, чтобы правый конец шатуна двигался по горизонтали (пунктирная линия на схеме).
Да, достаточно просто нужную форму поверхности просчитать математически, и, если кому-то понадобится, могу привести расчёт. Поэтому этот пример считаю чисто показательным, ведь механизмы бывают и сложнее, порой нужную траекторию аналитически получить в принципе невозможно.
Итак, я тут сделал примитивные детали. На правдоподобность механизм не претендует, всё сильно упрощено, ибо пример.
Источник – http://engineerblog.ru. Если копируем, оставляем прямую ссылку на источник.
Опора:
Коромысло:
Шатун:
Поставил точки PNT1 и PNT0. Пусть PNT1 должна ходить по прямой, а для PNT0 нам нужно получить траекторию. В реальной задаче были ещё детали в самой кинематической цепи, тут опять упрощаем.
Соберём механизм.
Опору закрепляем «по умолчанию» (default, больше люблю английскую версию):
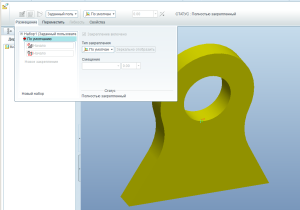
Для шатуна используем закрепление «Ось» (Pin). Указываем выравнивание оси (Axis alignment) и перемещение (Translation. Просто совпадающие плоскости). Ограничений на вращение ставить не будем.
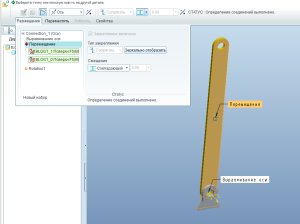
Ну и вставляем шатун. Первый набор закреплений – Ось:
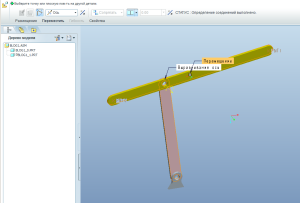
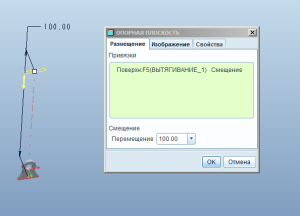
Теперь думаем, как лучше задать движение правой токи шатуна в горизонтальной плоскости (наше условие). Можно вернуться в опору и создать в ней плоскость, с которой впоследствии связать точку PNT1. Так и сделаем.
Напомню, все размеры взяты наобум. Редактируем определение шатуна: создаём новый набор Общее – Точка на поверхности (General – Pnt on surface). С таким же результатом можно выбрать закрепление Подшипник, но когда что-то более хитрое, чем сопряжение по оси или плоскости, я предпочитаю Общее.
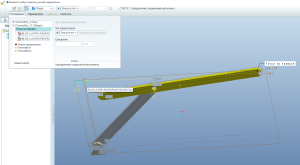
Теперь можно вручную всё подвигать и удостовериться, что всё работает, как надо. Учитывая только то, что у такого механизма при одинаковом угле поворота коромысла может быть два положения. Но мы всё видим и не ошибёмся 🙂
Теперь нам нужно проанализировать механизм. Точка PNT1 уже ходит по нужной нам траектории, осталось сделать деталь с поверхностью с нужной нам формой.
Идём в Приложения->Механизм (Applications->Mechanism). Ставим сервопривод – такая кнопка с синей растянутой спиралью на правой панели. В качестве оси вращения выбираем ось вращения коромысла:
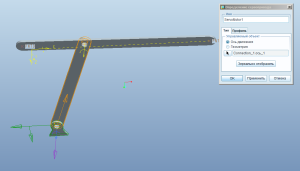
Идём в профиль двигателя. Мы меняем положение от одного определённого значения угла поворота коромысла до другого, поэтому для задания закона движения используем таблицу. Текущий угол можно посмотреть, нажав кнопку, на которую я указал красной стрелкой на скриншоте. Там же можно поменять ориентиры для определения угла и задать пределы его изменения, а также нулевое положение (это просто настройки самой оси вращения, они же есть при задании закрепления с этой осью).
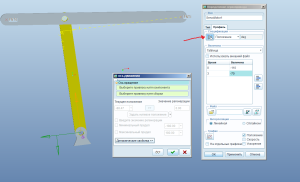
Теперь возвращаемся в Приложения->Стандарт. Нужно создать новую деталь, по которой будет ходить точка (в нашем упрощённом случае). Вставить->Компонент->Создать… Создаём новую деталь, называем, как нам надо, закрепляем По умолчанию (Default).
Теперь у нас есть закреплённая пустая деталь, в которой создадим кривую. Возвращаемся в Приложения->Механизм. Необходимо сделать анализ положения механизма. Для этого жмём кнопку Анализ механизма в правой панели, появляется окошко:
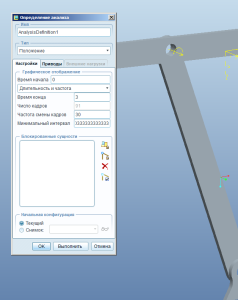
Время от 0 до 3 секунд (время работы указано в той таблице в сервоприводе, больше не имеет смысла). Чем больше количество кадров, тем больше будет точек в сплайне траектории. Жмём Выполнить и смотрим, как работает механизм. Правильно? Жмём Ок.
Теперь ключевой момент. Вставить->Траекторная кривая (она же Trace curve). Выбираем в появившемся окне нашу пустую деталь, точку, траекторию которой описываем, и результат анализа, который только что совершили:
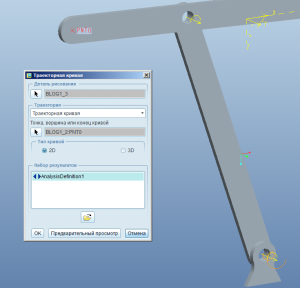
Теперь можно нажать на Предварительный просмотр, а можно сразу Ок.
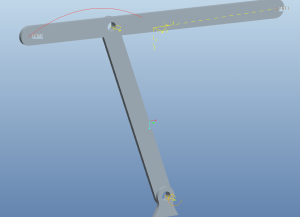
Траектория готова. Открываем саму деталь, которая была пустой.
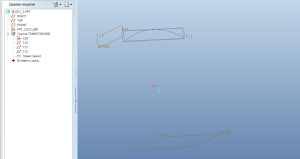
Как видим, мы получили эскиз (sketch) и три ортогональные плоскости, к нему относящиеся и объединённые в группу. Кстати, если бы при построении кривой мы бы выбрали 3D, а не 2D, то получилась бы пространственная кривая, а не эскиз. Но тут нам лучше эскиз подходит.
Ну теперь правим эскиз и делаем деталь. Кстати, в эскизе видны все точки, и они ни к чему внешнему не привязаны. То есть при любых изменениях деталей и механизма придётся делать другую траекторию, и наша деталь, которую мы сейчас сделаем, меняться не будет. Оно и к лучшему.
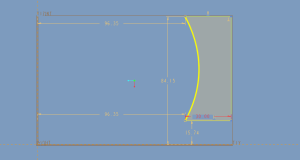
Ну а теперь выдавливаем эскиз, работаем над деталью. Допустим, всё сделали.

Возвращаемся в сборку и видим:
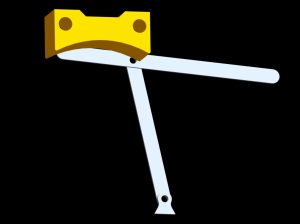
Теперь осталось пересобрать механизм и убедиться, что правая точка движется по прямой.
Я заменил второй набор закреплений шатуна на Ползунок (точка на линии).
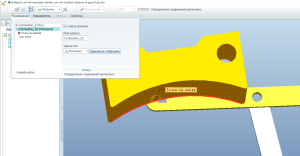
Возвращаемся в механизм. Создаём два измерения для точки PNT1: положение по X и по Y. Для этого нажимаем кнопку, на которую я указал на скрине.
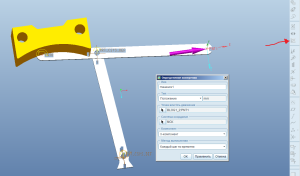
Создали. Теперь делаем снова анализ механизма. Так как я детали я скруглил концы траектории, то Pro/ENGINEER скажет об ошибке при выполнении анализа. Мы жмём продолжить и не паримся – крайние точки нас не интересует, мы заранее траекторию с запасом делали. Возвращаемся в окно измерений и делаем Измерение по измерению.
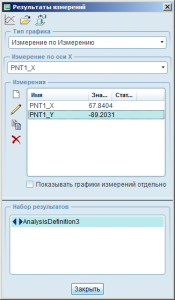
Получаем график (годограф фактически):
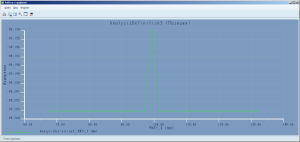
Небольшой пик (смотрим единицы – это миллиметры) для меня был неожиданностью, но это, видимо, погрешность программы. Суть в том, что точка движется горизонтально, что нам и требовалось.
Всем чмоки, ваш Димон.



Занятно, даже захотелось попробовать. Применять пока не тянет. Несколько лет назад пришлось кулачок в форме логарифмической спирали разрабатывать, обошелся имеющимся AutoCAD 2000. Это просто: Excel —> текстовый файл с координатами —> скрипт —> сплайн. Количество узлов — по настроению. А чтоб моя плоская и не слишком сложная кинематика понаглядней была, использовал простенькую и бесплатную программу «SAM 5.1». Хотя, признаю, в WF это будет солиднее и красивше выглядеть, начальству понравится.
С уважением
Borg, спасибо за комментарий!
Тоже разрабатывал как-то кулачок для определённого закона движения, там две архимедовы спирали уравнениями задавал. В ProE можно также и через Excel точки импортировать, причём по точности разницы особо не будет – и точки, и уравнения в итоге приближаются к сплайну.
А можно подробнее, что за программа SAM?
Приношу извинения, что так долго не отвечал, но откуда мне было знать, без уведомления, что мой скромный комментарий вызвал вопрос?
http://www.artas.nl/en — проверил, работает. Нормальная программа платная, но есть 4-недельный демо. Для моих более чем скромных запросов хватало ее время от времени заново инсталлировать.
С уважением
Borg