UPD от 25.02: выложил результаты работы программы
Появился тут ещё один кадр, который делает совершенно новый антивирус, как в своё время кое-кто сделал свою совершенно новую ОС (все помнят болгенос?). Нет времени и желания сейчас всё расписывать, да и не в антивирусе дело. Курите статью на хабре про парня, который написал свой крутой антивирус: http://habrahabr.ru/post/170487/ . Комментировать ничего не буду, ибо не хочу, антивирус и антивирус.
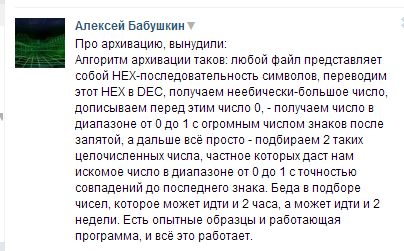
Также этот человек предлагает алгоритм архивации, который сможет сжимать фильмы размером 2ГБ до 2-3 кБ (на шесть порядков меньше!), и с помощью него можно будет поместить весь интернет на флешку. Как и антивирус (подробности в том самом интернете), такое заявление достаточно забавно. Итак, что же нам предлагает Алексей Бабушкин (взято с его страницы вконтакте):
(Вникни, читающий, в текст на картинке.) Ну кто я такой, если в три часа ночи не стану доказывать, что как и вечные двигатели, которые нарушают закон сохранения энергии и законы термодинамики, такой алгоритм работать не будет. По крайней мере ничего так существенно сжать не получится.
Итак, я открыл MATLAB, люблю его. Давайте возьмём произвольные шесть байт. Почему именно шесть? Достаточно показательно, и числа не выходят за границы типов данных матлаба. Итак, шесть байт это 256^6 возможных комбинаций. В 256-ричной системе это 6 символов, а в десятичной это число можно записать с помощью lg(256^6) знаков. Доказывать, почему так, не буду, это достаточно очевидно. Итак:
>> log10(256^6)
ans =
14.4494397918711
Чтобы дописать «число 0», делим на 10^15. Недолго думая, написал алгоритм перевода в десятичную систему координат со сдвигом на 15 знаков:
format longG % вывод: 15 знаков после запятой a=fix(rand(6,1)*256); % вектор из шести байт st=[0 1 2 3 4 5]; 256.^st*a/10^15
Итак, вот числа, полученные с помощью кода выше:

Осталось дело за малым. Пусть наше число – a, и надо найти числа m и n такие, что m/n=a.
Алгоритм: начнём с n=5. По идее лучше с 2 начать, но мы не так и много потеряем: если что, m и n просто сократятся. Конечное n в цикле будет 10^15, так как у нас есть точно одна пара целых чисел: десятеричное представление тех шести байт и эти самые 10^15.
Пусть m в самом начале равно 1: первая пара это 1/5. Наша задача найти такое максимальное m при данном n, чтобы a-m/n было как можно меньше. Иными словами a>m/n и a<(m+1)/n.
Нашли? Если до сих пор a ни с какой парой чисел не совпало, увеличиваем n на единицу. m пробуем прежний, так как m/n<a, m/n>m/(n+1), следовательно, m/(n+1)<a, и всё числа, меньшие m из предыдущей итерации нам не нужны.
Так. Код написан, работает. Действительно, относительно долго. Для получения статистики запущу на ночь, чтобы «заархивировал» несколько 6-байтовых случайных последовательностей.
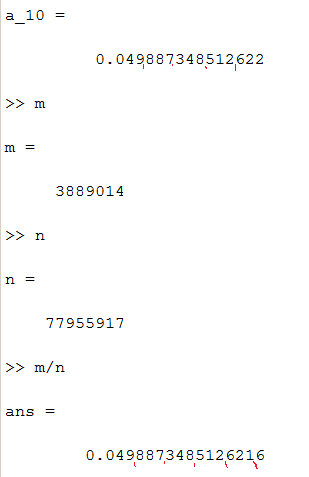
А сейчас приведу те результаты, что уже получил. Сами случайные байты:
>> a'
ans =
110 215 175 77 95 45
Полученный результат:
Шестнадцатый десятичный разряд округляется, пусть будет так. Без этого допущения сжатие будет ещё меньше.
Так вот: было 6 байт. Получены числа 3889014 и 77955917, которые однозначно определяют наши 6 байт. Теперь возьмём логарифмы по основанию 256:
>> log(m)/log(256)
ans =
2.73637162470509
>> log(n)/log(256)
ans =
3.27701939931803
>> log(m)/log(256)+log(n)/log(256)
ans =
6.01339102402312
Ололо, те же шесть байт. Это без учета того, что каждое число записывается своими байтами и мы округляем 2.73… и 3.27… в большую сторону. Итого 7 байт. Сейчас иду спать: на ночь оставляю работать программу. Пусть для эдак десяти наборов байт найдёт соответствующие пары чисел.
P.S. Код:
format longG % вывод: 15 знаков после запятой
for num=1:10
a=fix(rand(6,1)*256); % вектор из шести байт
st=[0 1 2 3 4 5];
a_10=256.^st*a/10^15; % число-отображение вектора
m=1;
for n=5:1:10^14 % увеличиваем n
while (a_10>double(m/n))
m=m+1;
end
m=m-1;
% находим такое максимальное m, m/n<a
if (a_10-m/n==0) % совпало!!1
break;
end
end
% выведем наш результат:
[a_10 m n m/n]'
end
UPD от 27.02. В этом коде не учёл округление, см. рабочий в новом посту про алгоритм.
Запускаю. Ни хрена этот алгоритм не сжимает. А сожмёт только в редком случае, когда число-отображение очень сильно сокращается. Насколько это может быть часто? Это и выяснит наша ночная программа.
Полезные ссылки: Эффект Даннинга — Крюгера — Википедия
Спокойной ночи.
Мдда…алкогоритм ппц. Это как ляпнуть мол я произвольный размер могу «сжать» в MD5-конТролль-ную сумму … а потом десятки тысяч лет «распаковывать» путем полного перебора. ^^
А ведь еще есть коллизии! Распаковал, да не то, что упаковал.
ну всяко коллизий меньше чем попыток подбора. тем более что можно снабдить «дописать» файл доп контрольной суммой или еще проще сделать выборку исходный байт что тоже значимо уменьшит количество коллизий)
…ну это все просто вариации на тему)
тут то хоть у тя будут все теже 16 байт хеша + служебка (и милльён лет на реверс ^^) а в алкогоритме попова помоему надо хранить еще больше чем исходник))
Ну это же очевидно! Нужно добавить ещё контрольную сумму, и ещё, и ещё..
Именно так появляется компромат на ВикиЛикс 🙂
Автору спасибо за «разбор полетов» 🙂
Awesome) Ждем результатов)
это че сказать,а число искомое общимножетель как ты говоришь, но данный множетель, в многих цыврах совподает, потом этомы будем перебирать при рапоковке дофига времени удет.
фильмы размером 2ГБ до 2-3 кБ так сжать можно но рапокуется до фига лишних терабатов, лучше рекурсию исползовать
Не, чувак, ты хрень сказал
Конечно, те же 6 байт. Ведь все действия, которые произведены, ничего, кроме другой формы сжатия нам не дадут.
*Формы записи. Простите, задумался над формулировкой и опечатался.
Ну же, ну же? Ждем с нетерпением результата вашей ночной программы!
Вот тоже жду, MATLAB ещё считает 😀
целочисленные числа……omfg
Это больше похоже на алгоритм хеширования(причем очень убогий, с туевой хучей коллизий) чем сжатия.
Да вы что так все усложнили? Такое представление числа — единственно. Очевидное представление такого числа — это дробь, в числителе само число, в знаменателе — 10 в степени порядка числа. Если числитель нечетный и не делится на пять — то никакого сокращения дроби не будет — а значит в 40% случаев архиватор ничего гарантированно не сожмет.
Гораздо интереснее случаи, когда при таком «сжатии» размер файла вырастет. Ведь автор предлагаэ хранить два числа — числитель и знаменатель. Вот, например, файл с содержимым «123» будет представлен числом 0.123, и минимальные числитель и знаменатель по методу Бабушкина для него будут 123 и 1000. Вуаля, файл увеличился в 2,3 раза 🙂 А ведь 123 — это даже не простое число.
Я вот все думаю, что мне этот архиватор напоминал? А напоминал он мне уже известный архиватор Лыщенко
Спасибо, посмеялся)
Но зачем полный перебор, если есть цепные дроби: http://en.wikipedia.org/wiki/Continued_fraction#Best_rational_approximations
Искал что-то такое, почитаю, спасибо
А если квантовый компьютер использовать?
Действительно не сильно понял зачем тут перебор. Разве после того как мы записали длинное число X и посчитали его длину L, результат не будет просто X / GCD(X, 10^L) и 10^L / GCD(X, 10^L)? А чтобы найти GCD достаточно заметить, что надо посчитать только 2ки и 5ки в составе X.
Суть в «точности совпадений до последнего знака» (дожил, защищаю алгоритм Бабушкина).
Например, у нас не 10^15, как я использовал выше, а просто 100000.
Возьмём исходное число 0.57059, это 57059/100000. Наибольший общий делитель, как верно подмечено, – единица, так как двоек и пятёрок в 57059 нет.
Далее, попробуем поделить на 13: из 57059 получаем 4389.15384615385, сокращаем до 4389, из 100000 – 7692.30769230769, что сокращаем до 7692.
Итого: 4389/7692 = 0.570592823712949. Сокращаем до нужного нам знака, получаем исходное 57059.
Кстати, эта дробь ещё и на 3 сократится: 1463/2654. И не факт, что это – дробь с наименьшими числами, которая в приближении даст исходное число. Числа вообще взяты наобум.
Только всё равно на запись последней дроби нужно около 2.73 байт, а на запись оригинала – 1.98 байт. Нецелое число байтов – некая абстракция, всё равно обобщать до чисел, в которых 2ГБ фильма записано.
Я вообще поражаюсь, что в блоге инженера (судя по названию) нет ни единого упоминания про арифметическое сжатие (http://ru.wikipedia.org/wiki/%D0%90%D1%80%D0%B8%D1%84%D0%BC%D0%B5%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D0%BA%D0%BE%D0%B4%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5). То, что это чудо описало ― стандартная вводная на первой лекции, посвящённой этой теме.
У нас и не читали такого. Это к инженерам-программистам, наверное, больше относится
Это основы Теории информации. Мне казалось, всем более-менее причастным к IT её читают.
Думаю не пройдёт с видео такое сжатие — ПРОВЕРЕНО !!!
С текстом — пройдёт ,а видео порежет, вот игра есть
kkrieger http://theprodukkt.com/kkrieger
Там алгоритм использует графику которая моделируется из ОС — может Бабушкину поможет…..
Ссылка не работает, а игру видел в своё время 🙂
Да и с текстом этот алгоритм вряд ли справится, он сильно отличается от других алгоритмов, которые реально сжимают
Помнится, сильно удивлялся в свое время, как в 64 килобайта памяти на компе Commodore в какой-то версии «стрип покера» втиснули «типа видео» аж на 30 секунд 🙂
даёшь в комменты видео из стрип-покера)
Это было очень давно и сейчас ни ютуб, ни поисковик не помогают с нахождением именно того покера или аналога с «видеоклипом». Сдается мне, что это был какой-то хак игры из 90х годов.
Я просто надеюсь, что найдутся люди, подтверждающие что «Коммодор» мог проигрывать «клипы», если их так можно назвать. Возможно были аналоги на других подобных машинках?
Может, там графический чип SID как-то особо извращенно хакнули? Вообще там результат не особо отличался по качеству от того «видео», которое наблюдалось в позднем софте для 286 проца, и такого же размера с почтовую марку, без звука естественно. На 286 в какой-то проге я смотрел старт ракеты на Луну или что-то подобное.
Вот нашёлся видеоплеер для Комода 🙂 Правда, там на машинке 16 метров ОЗУ 🙂
http://www.youtube.com/watch?v=IXLv7UosQXs
Просто мысль — она нематериальна в нашем мире а для неё — нет размеров она бесконечна.
А вот вся инфа на компьютере это ноль еденица и висячка ,которые в свою очередь яляются потоками энергии с разницей напряжений ,то есть материя.Короче если этот алгоритм сделаеш — считай — исскусственный интеллект создал,Энштейн отдыхает,все законы физике можно выкидывать ,а математику сделать не просто расчётной наукой ,а считай инструментом для материализации — то — есть,если полочится тебе парень Бабушкин нужно памятник во весь рост из золота ставить …..
http://programki.net/program.php?pr=522
Эта насчёт алгоритма сжатия прога картинки делает цифрами.
http://yadi.sk/d/kr2drNRO2tA8Q
Боюсь тестировать лень переустанавливать систему ,извини.
Это насчёт антивирус «Иммунитет»
http://yadi.sk/d/PPC_WPmL2tA6s
http://yadi.sk/d/2aoy72H52tA6W
Мне напоминает этот алгоритм сжатия художника Малевича с его картиной «Чёрный квадрат» — он нарисовал в нём ВСЁ от начала сотворения до конца ,можно представить что там в этом и всё видео которое снято и ещё не снято, ведь только человеческое воображение может это всё увидеть в его работе. Советую найти книгу «СИЛА ВОЛИ» автор-Премудрый Соломон ,последний кто её держал в истории -Григорий Распутин, а из современников есть такой человек который занимается наукой суггестологией — товарищ Игнатенко, он может помочь, только это будет очень дорого стоить — деньги для него ерунда ,жизнь — дороже.
Одного не пойму, уважаемые, над чем, собственно, спорите?
Алгоритм не имеет к Дедушкину никакого отношения, я про него читал еще в средней школе (году в 1986) у Мартина Гарднера, кажется, в «Есть идея!»:
«…инопланетяне вступили с землянами в контакт, собрали все наши знания, а потом на «палочке» сделали зарубку. На вопрос «чтозанах?» ответили то же самое, что Дядечкин — два числа, расстояния от зарубки до концов «палочки» при делении дадут «неетически-большое число», в котором закодирована вся эта информация огромного объема»
Наконец-то! Думал самому придется писать, что алгоритм есть ни что иное, как легенда об ассоциативном кодировании =)
Ну вот и объяснение дежа вю. Это просто мозг раскодирует соломинку, в которой зашифрована вся твоя будущая жизнь 🙂
Этот Бабушкин даже не прохиндей — просто несчастный человек с покореженной психологией.
Немного по поводу уже вашего алгоритма по поиску дроби. Я извиняюсь, но это пипец (если вы не шутите). А не проще просто взять начальное число и найти его НОД с 10^n по алгоритму Евклида? Ну а затем деля начальное число и 10^n на это число получим как раз дроби для точного представления (число-то имеет конечное число разрядов и соответственно рационально).
Если реализовывать таким образом сжатие с потерями, то можно использовать алгоритм для поиска подходящих дробей — будет быстро и гарантированно оптимально.
А Бабушкин — мошенник обыкновенный, ну и плюс «сынок».
Это верно, если искать точную дробь, нам же подойдёт наименьшая по числителю (или, если угодно, знаменателю), которая при округлении до соответствующего знака даст нужную нам.
А то, что в этом коде ищет точное соответствие, – ступил, уже исправлено и проверено в работе в новом посте. В любом случае я подразумевал, что должно округляться.
«алгоритм для поиска подходящих дробей» – что подразумевается?
>> «алгоритм для поиска подходящих дробей» – что подразумевается?
http://ru.wikipedia.org/wiki/Цепные_дроби
Подходящая дробь — это как раз округление дроби для числа в нормальной форме
Оставьте Бабушкина в покое. У человека с женским полом проблемы, там не только крыша съедет, там фундамент заиграет, а он при этом сын большого человека. Отстаньте от него, прекратите. Будьте милосердны, в конце концов.
НЕТ НЕ ОТСТАНЕМ
Конечно, идея хранить числа в текстовом формате с неизбежной потерей 2 байт на разделители, это глупость.
Но все дело в том, блоки какого размера шифровать. Поскольку с увеличением длины блока размер выходных данных растет медленнее.
Число с плавающей точкой четверной точности — 16 байт (128 бит), это примерно 40 десятичных знаков. Спасибо, jcmvbkbc, напомнившему про цепные дроби. Подходящие дроби с требуемой точностью 1Е-40 появляются на уровне от 15 до 20, размер числителя p и знаменателя q на границе 32-33 битов, будем считать, что каждый займет от 1 (теоретически) до 5 (практически) байт. Добавим еще один служебный байт, в тетрады которого занесем длину чисел p и q. Итого 11 байт из 16.
Это, конечно, не 2кб из 2гб, но все же сжимает. Если же извратиться и увеличить размер блока, то прибавка к пенсии будет еще существеннее.
Это все же оценка, ибо надо проверить, как будут проходить вычисления на такой точности.
Расчеты проводились в Excel, у него траблы с повышенной точностью, но ошибка Н/Д выходила крайне редко.
Да, проверил. Точности Excel не хватает для категоричного утверждения. Надо будет проверить в чем-либо посерьезнее. Однако, более медленный рост выходных данных с ростом размера блока налицо.
А где предлагалось хранить в числовом формате?
Я считал объем, занимаемый десятичным числом, исходя из следующих соображений.
Число N можно представить log(n, 256) или ln(N)/ln(256) байтами. Получаем нецелое число – округляем в большую сторону. Например, числа от 1 до 256 записываются одним байтом, до 65536 уже двумя. Чем больше число, тем меньше значения имеет округление. Если работаем с маленькими числами и не округляем, то получаем примерную картину и для больших чисел – я исходил из этого допущения.
>> А где предлагалось хранить в числовом формате?
Бабушкин вроде бы и предлагал. Я так понял из ролика, где было интервью. В любом случае, второй раз слушать не буду, поэтому если не прав, то сорри.
>> Чем больше число, тем меньше значения имеет округление.
Не совсем так. Чем длиннее блок данных, тем больше в нем должно быть верных цифр и меньше погрешность округления.
Блин, Бабушкин не говорил о числовом формате, именно о текстовом — хранение выходных числовых данных в текстовом формате. ЕМНИП
По-моему, зря копья ломаются. Бабушкин явно чайник в теории информации, но в целом он гений, просто он еще не понял своего предназначения. Это надо уметь, создать полную ерунду с научной точки зрения, но при это привлечь к себе внимание огромного количества людей. Это не каждому дано.
Порой то, что хорошо продаётся, хорошо продаётся только потому, что хорошо продаётся (и подаётся) 🙂
Сам диву даюсь
Вот вы пишете всё это,вроде и по-русски,а я понимаю только предлоги и междометия. Доказываете что-то.. Басню Крылова помните,про слона? Так вот,слон в нашей басне это немалого размера грант (400.000р???),который откусил этот самый студент за своё словоблудие. Расслабьтесь и попейте пива по скайпу за здоровье и щедрость всенародно избранного..
Михаил, мы пиво и без скайпа умеем пить.
Алгоритм действительно сжимает данные, не как заявлено, но сжимает. Вопрос в его реализации — числа можно сохранять не только по байтам, но и по битам. Главное — это в лемме Лыщенко — как восстановить то, что сохранил. Рядом лежит другой вопрос — в оптимальности этого способа. Этот Бабушкин ничего нового не открыл, полагаю, что эффективность сжатия хуже, чем в стопицот лет используемых методах.
Как семестровая — тянет. Коммерческой прибыли ноль.
Парень получил грант — ну может придумает что-нибудь, а не пиво пропьет.
А вот его учители арифметики и есть лохи, которые америку в XXI веке заново открыли.
Мне чет кажется что тут натуральный троллинг и PR качинг со стороны Бабушкина…или я ошибаюсь?
Кстати, по ссылкам на Хабре нашел тот самый фрагмент из Гарднера:
http://golovolomka.hobby.ru/books/gardner/gotcha/ch2/10.html
Доброго времени суток, я, вероятно, не понимаю гениальности этого алгоритма. Пожалуйста, объясните мне в чем я не прав. Грубо говоря, Бабушкин предлагал переводить из двоичной (шестнадцетеричной) системы в десятичную… Потом писал «0,» _ «число в десятичной системе». Т.е. для одного байта это выглядит в духе 0,xyz…. Для двух 0,qwertyu (буквы-цифры от 0 до 9)… В результате он получает число от 0 до 1…. И предлагает вместо него хранить два других целых числа, частное которых дает нам его число (с интересующей нас точностью). Пусть у нас для каждого возможного числа от 0..1 (с какой то точностью) найдена пара целых… У нас получается биекция. Из чего следует, что записать дешевле чем изначально не прокатит… По крайней мере у меня в голове именно так.
Или можно и по другому…. Пусть у нас есть число 0,сколько-то знаков после (пусть N знаков).
Т.е. для десятичной системы возможно N^10 вариантов записи этой последовательности… Пусть у нас каждая дробь дает уникальное рациональное число (что конечно же очень грубое и нехорошое предположение). Тогда если возможно записать меньше чем m*n вариантов этими дробями где m и n максимальные числитель и знаменатель соответственно вот и выходит что в общем-то, если брать некое число длиной N, то m*n=N^10 (т.к. дробей должно быть n^10) … А это значит что записывая m и n, мы в общем случае ничего не выигрываем…. Т.к. архивировать нужно будет через блоки зараннее известной величины… В противном случае возникает проблема, если вы вдруг заархивировали два файла разного размера таким образом и получили, например, 5/17 в обеих случаях, то неясно как разархивировать эти два числа.
Если я глубоко ошибаюсь, то поясните в чем. Буду искренне благодарен. Просто тратить время на эксперименты такой идеи мне жалко…
Скорее даже не биекция, так как одному исходному набору байт может соответствовать несколько дробей. И тем более это говорит о том, что сжать ничего не получится)
Тогда если возможно записать меньше чем m*n -слово «если» для понимания написанного стоит убрать, ошибка мешает понять, что я имел ввиду…
Жаль, что я не узнаю ответа по поводу того что писал )… Но меня больше другое волнует… В вашем примере положим файл как раз размером три байта. Получим два числа, пусть даже из тех 13% удачных ), а как вернуть исходный файл, т.е. как определить что файл был именно 3 байта, а не 3килобайта, например… Ну т.е. разве не придется тратить ставить доп отметку о размере файла? Очень прошу ответить.
Всё так, но когда байта уже не три, а больше, отметка не займёт много места
Думал, что мои комменты удаляют ))) Т.к. на блогах обычно не пишу ). Просто это переходит все разумные границы ). Спасибо за быстрые ответы ).
По теме:
Да. да там вообще сюрьективное отображение… Просто, если зараннее фиксировать длину блока, то можно договориться так, чтобы была биекция. Т.е. пусть нам нужно число 0,666666, то мы можем договориться, что за него отвечает дробь 2/3, а дроби 4/6 6/9 и прочие дроби, входящие в класс эквивалентности 2/3 мы считаем несуществующими. Ну проще говоря не используем ). Но сути это не меняет, т.к. тип данных «(число, число)» будет занимать неменьше чем исходный тип данных даже при правильной реализации… Как раз -таки из-за биекции… Конечные множества должны быть равны по количеству элементов. Я даже не знаю как толкого объяснить такую жесть… Просто здравый смысл подсказывает, что если бы такой архиватор существовал, то любой файл можно было бы пожать до 0 бит…. Парень замахнулся сжать произвольный файл, т.е. и собственной архивации тоже сожмет ) А идея создать подобный бред меня когда-то тоже посещала, но потратив на нее какое-то время, я пришел к выводу, что это невозможно )). Только было одно существенное отличие… Я не втирал ничего сми… И меня крайне злит вся эта ситуация — с архиватором и так понятно. Но вот с антивирусом, судя по тому, что я успел почитать и даже послушать, а это весьма и весьма немало (и пусть там не все правда) Но он непохож на тролля… Он искренне убежден в том, что ему завидуют, что он — сама гениальность и т.д. Нет, конечно, спору нет писать батники в несколько тысяч строк я бы не стал, да и не смог бы, в силу бесполезности такой работы… Про грант еще могу пережить, хотя как его выдала комиссия МФТИ (один из лучших вузов, как по мне-грустно, что к этой истории он имеет отношение) остается для меня загадкой… Это ж не пивка дать попить, а 400к. Но что убивает меня больше, так это продажа этого «творения»… Все логично, все четко, сказал бы я — молодец. Да вот не скажу, потому что все это по меньшей мере неправильно, и такой развод не должен сходить с рук. А если ты дурачок, то это не освобождает от ответственности… Надеюсь, что шум вокруг этой ситуации скоро поутихнет, и все получат по заслугам (хотя мечтать невредно)….
Не, никто не удаляет. Просто комментарии от новых авторов модерируются.
Спасибо за комменты 🙂
> Надеюсь, что шум вокруг этой ситуации скоро поутихнет, и все получат по заслугам (хотя мечтать невредно)…
Увидим со временем
В полку прибыло. Пробовал реализовать этот алгоритм. Даже программу написал)
В общем, вся лажа начинается ещё тогда, когда автор предлагает приписать ноль и запятую. Десятичная дробь от числа — есть ни что иное, как это же число, делённое на десять в степени количества его знаков.
Моя программа предельно честно выполняет поиск методом «качельки» вокруг исходного значения. Тратит уйму итераций, грузит процессор, а в случае большого числа ещё и пожирает память страшными цифрами.
Конечно можно потратить кучу времени, которого и без того не много, придумать методы обхода счёта старших разрядов, ускорить процесс, снизить потребление ресурсов, но зачем? С тем же успехом я могу радикально упростить алгоритм, оставив только код, считающий десятку в степени количества знаков, выдать исходное число и полученное значение. Тем самым избавлюсь от лишнего звена в алгоритме — того самого ноу-хау автора, из-за которого весь сыр-бор. Конечно, степень сжатия будет составлять чуть более -100% ))) Т.е., исходный файл будет увеличиваться раза в два) А если оставить математическое представление второго числа, то такого не будет, но и сжатия не произойдёт.
Просто хотелось проверить нежизнеспособность алгоритма. В общем, ещё один Болген ОС)))
🙂
Десятичная система упрощает представление. Фактически в итоге мы находим два числа, записанные в 256-ричной системе (байтами), имея исходное в той же системе (3ГБ фильм). Суть ещё в округлении, тогда степень сжатия колеблется около 1, а как показал следующий пост, 1.1 для трёх байт.
[это всё моя интерпретация алгоритма]
че хотел, сказать чило общий множетель дробей то, то данный множетель может совподать во многих цифар, потом пака мы будем перебирать, на рапокавание дофига времени удет.
фильмы размером 2ГБ до 2-3 кБ сжать можно но распакуется до фига лишних терабайтов, лучше использовать рекурсию.
Да ладно…уже не актуально. Говорят, этого умника сегодня самоубиенным нашли. Инфа не сто процентная, вроде как ждать надо официальных статей от СМИ. Но ифна такая по нету проходила.
Печально, если так. Надеюсь, что всё-таки утка
Или попытка запустить таковую. Не нашёл никакой инфы, которая по нету проходила
Суть в «точности совпадений до последнего знака» (дожил, защищаю алгоритм Бабушкина).
Например, у нас не 10^15, как я использовал выше, а просто 100000.
Возьмём исходное число 0.57059, это 57059/100000. Наибольший общий делитель, как верно подмечено, – единица, так как двоек и пятёрок в 57059 нет.
Далее, попробуем поделить на 13: из 57059 получаем 4389.15384615385, сокращаем до 4389, из 100000 – 7692.30769230769, что сокращаем до 7692.
Итого: 4389/7692 = 0.570592823712949. Сокращаем до нужного нам знака, получаем исходное 57059.
Кстати, эта дробь ещё и на 3 сократится: 1463/2654. И не факт, что это – дробь с наименьшими числами, которая в приближении даст исходное число. Числа вообще взяты наобум.
Только всё равно на запись последней дроби нужно около 2.73 байт, а на запись оригинала – 1.98 байт. Нецелое число байтов – некая абстракция, всё равно обобщать до чисел, в которых 2ГБ фильма записано.
Ответить
я ничего толком немогу понять почему делим на тринацать
и снова данное число, и че нам дает это.
57059/13=
4389/57057=7692.30769230769 аткуда 57057 непонятно
потом мы
делим сокротив и что ето нам дало тоже самое
4389/7692 57059
прошу обиснить где сжатие если тоже самое осталось
и аткуда 13 и 57057
Да он изобрел арифметическое кодирование. Сжатие чуть лучше кодирования Хаффмана, особенно когда один симол встречается гораздо чаще других. Но, конечно, ни о киких шести порядках речи не идет.
Правда? Что-то я не уверен
А у меня свой алгоритм есть, только кривой он и не дописан и не реализован. Даже в ФСБ рассматривали.
Насколько эффективен?
Примерно настолько же, насколько заявил предыдущий автор. Гигабайты можно сжимать в килобайты без потерь. Этому способствует многомерная двоичная матрица. Описание можно прочитать здесь: http://vk.com/doc34297903_146501132?hash=21d5952ae48bf79bf8
Там криво написано, «на колене». Что — то надо удалить, что — то упростить и что — то дополнить. Сейчас описание в вордовском файле «как есть». А ещё есть аналитическая программа и макрос, генерирующий по суммам исходных данных крест из единичных битов.
А знаете в чем прикол? В том что автор и читатели этого блога похоже не далеко ушли от Бабушкина в понимании архиваторов.
За счет чего сжимает архиватор? За счет того, что он делает предположение об избыточности данных в сжимаемом файле. Например, если взять текстовый файл, то каждый символ кодируется 8 битами. А если в файле только латинские буквы и пробелы (27 разных символов), то под один символ достаточно выделить 5 битов (можно закодировать 2^5 = 32 разных значения). То есть в таком файле есть избыточность, которой может воспользоваться архиватор чтобы сжать файл. Никакой архиватор не может сжать файл без избыточности — например белый шум (случайные байты) или заархивированный файл, в котором избыточность уже устранена. Именно поэтому ваши доказательства непригодности этого алгоритма для сжатия случайных байтов бессмысленны. Их не сможет сжать ни один архиватор.
Нахождение избыточности в общем случае это нетривиальная задача, поэтому нет универсального архиватора, который сжимает любые данные лучше других. Для конкретного типа данных человек определяет как устранить избыточность и пишет архиватор для конкретного типа данных. Какие данные хорошо сожмет архиватор Бабушкина? Те что представляют собой дробь двух чисел.
Пример: нам нужно сжать 12 байт
0х20 0х0F 0x55 0x5A 0x1E 0x53 0x46 0x04 0x28 0x34 0x56 0x22
переводим их в десятичный вид и добавляем 0.:
a = 0,321585903083700440528634
находим n/m = a
это 73 и 227
мы сжали 12 байтов до 2!
возьмем следующий формат архива: первый байт это длина исходного файла, второй байт это число n, третий это число m, итого 3 байта на архив. да такой формат не очень универсален но это просто показать что метод работает, а формат можно доработать. кстати двумя числами 73 и 227 мы могли сжать хоть гигабайт данных, если они представляют собой их частное.
да насчет самого алгоритма
как мы видим он слишком специфический
хоть он и позволяет сжать гигабайт до нескольких байтов в некоторых случаях (в миллиард раз))
но вероятность встретить такой удобный исходный файл мала
так как мы не можем заранее определить хорошо ли сожмется файл, то пользование таким архиватором превращается в лотерею — то ли сожмется, то ли разожмется, при этом работать он будет по видимому очень долго
поэтому алгоритм практически бесполезен
На самом деле, можно было обратить внимание еще вот на что. Возьмем набор из примера автора, я возьму уже переведенное «число в диапазоне от 0 до 1 с неебически большим числом знаков», то есть:
a = 0.049887348512622.
У этого числа 15 знаков после запятой. То есть, дробей с 15 знаками после запятой — 10^15. Отображение «обыкновенная дробь — десятичная дробь» сюръективно, и для кодирования всего диапазона таких дробей нужно как минимум 10^15 обыкновенных дробей. Обыкновенная дробь будет парой чисел, каждое из которых, очень грубо говоря, можно будет выбрать 10^8 вариантами. 256^6~3*10^14, плюс еще нужно хранить разделитель этих двух чисел, чтобы знать, где первое кончилось и началось второе. Так-то.
Верной дорогой шел Бабушкин, но алгоритм, предложенный им, известен уже давно и выглядит он следующим образом:
Возьмем простой стержень и сделаем на нем всего одну зарубку, такую что деление длинны одной части стержня на всю его длину даст нам одно большое число (по количеству знаков после запятой, а не по величине), которое может кодировать всю структуру вселенной во все времена.
Получаем абсолютное знание.
Правда у алгоритма есть некоторые недостатки. Практические — точность измерений и постановки зарубки. Теоретические — возможно пространство вселенной дискретно, а не непрерывно.
Ну если пространство вселенной дискретно, то и точка постановки зарубки дискретна, тут как раз проблемы нет)
вообще существует бесконечное сжатие, без потери качества, и можем сжать 1гб в 15 байт, и не важно какого качества файл любой можно так сжать, и разжать, и без потерии качества.
Я знаю алгоритм лучше: берем любой файл с любым размером и алгоритм таков:
читаем файл и пишем в результате на выходе 5 байт «хуита»
вот и все конечно немного страдает точность но в общем нормально
подходит и для музыки и для почти всего.
По мне так примерно такой же 🙂
И так я сожму свой программой по-своему алгоритму без потери качества.
Уменя есть фото в формате .jpg для теста сейчас я её сожму и так сжать, сжать, сжать……..
И получилось 17.7 раз
Было 16001 Байта стало 904 Байта.
Проблема не в алгоритме сжатия, проблема в не понимании простой и понятной вещи:
предположим мы хотим сжимать любые файлы (возмём стогий размер для упрощения представления) размером 1234567890 бит (сколько это в байтах считайте сами, это не важно)
Это значит общее колличество этих файлов будет равнятся 2 в степени 1234567890 — то есть это будет колличество возможных вариантов исходных файлов
После сжатия мы получим какой то результат — данные (то есть результирующий файл скажем .xrar )
Но общее колличество результатов ни как не может быть меньше чем колличество исходных файлов
То есть если мы сохраняем результат сжатия так же в двоичной системе, то общее колличество возможных результатов сжатия будет равняться также 2 в степени 1234567890
На каждый вариант исходного файла — один вариант результирующего! А иначе коолизия, то есть два разных исходных файла после сжатия выдали бы один и тот же результирующий файл
Вот и вся математика…
Архивация в принципе существует. Может быть такое, что из одного фала получится два разных файла — разные инструкции. Взять хотя бы «фотожабу». Один файл исходный и много разных вариаций.