[предыдущий пост по теме: Алгоритм архивации Бабушкина]
Короче, надоело мне ждать цикл в 10^14 итераций (напомню, что это для сжатия 6 байт). Долго. Немного переписал программу: сделал для трёх байт и учёл ещё одно условие, на которое не сильно обратил внимание в тот раз.
Вот пишете, что перебор в принципе не нужен, достаточно заметить, что дробь a/b, где a – двухгигабайтный фильм, а b – десять в какой-то очень большой степени, может сократиться только на 2 и на 5 (не по одному разу, конечно). Поэтому достаточно поделить оба числа на наибольший общий делитель, и дело с концом.
Небольшая оговорка: два числа (которые я уже обозвал в предыдущем посте, как m и n) не обязательно при делении должны выдавать всё наше исходное число: оно должно получаться при округлении результата до определённого знака.
Рассмотрим три байта: 236, 82, 219. В десятичной системе я их записал так: 0.14373612. Теперь найдём два числа: это 3948 и 27467, их частное равно 0.143736119707285, что прекрасно округляется. Но! Степень сжатия тут около 111,218%.
Итак, я немного переписал код в MATLAB. Это всё тот же перебор, только теперь числа оказываются искомыми, если их частное отличается от оригинала менее, чем на 0.5e-9. Иными словами, если округление приведёт к оригинальному числу.
Итак:
format longG % вывод: 15 знаков после запятой
clear res;
res=0;
for num=1:10
a=fix(rand(3,1)*256); % вектор из шести байт
st=[0 1 2];
a_10=256.^st*a/10^8; % число-отображение вектора
m=1;
for n=5:1:10^8 % увеличиваем n
while (a_10>double(m/n))
m=m+1;
end
if (abs(a_10-m/n)<=0.5/10^9) % совпало!!1
break;
end
m=m-1;
if (abs(a_10-m/n)<=0.5/10^9) % совпало!!1
break;
end
end
% выведем наш результат:
l=length(res(:, 1))+1;
res(l,1)=a(1);
res(l,2)=a(2);
res(l,3)=a(3);
res(l,4)=a_10;
res(l,5)=m;
res(l,6)=n;
res(l,7)=m/n;
end
Это код заполняет переменную res. В данном случае получается что-то такое:
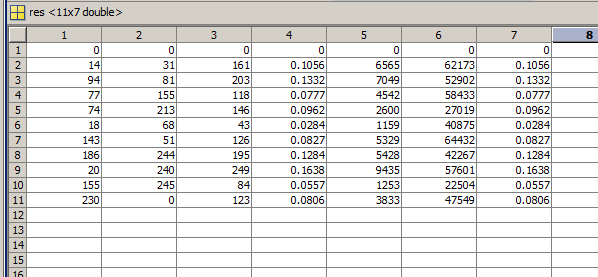
Первые три столбца – наши байты, потом их десятичное представление, найденные два числа и их частное. Пусть тут всё округлено до четвертого знака, это только при выводе округляется. Я сделал 1000 повторений и закинул оригинальные, не округлённые данные в Эксель, посчитав степень сжатия и количество байт, необходимое для хранения чисел m и n.
Итак:
- для хранения трёх байт, сжатых по данному алгоритму, нужно в среднем 3,32 байта.
- Средняя степень сжатия составила 110,78% (это когда «архив» больше оригинального файла на 10,78%).
- Всего несколько результатов были положительными. Максимальное сжатие: 52,42% для байтов 88, 217, 41.
- Сжатие 60%-70%: 2 раза из 1000.
- Сжатие 70%–80%: 8 раз из 1000.
- Сжатие 80%–90%: 17 раз из 1000.
- Сжатие 90%–100%: 103 раза из 1000.
- То есть реально что-то можно записать количеством байт, меньшим, чем оригинальное в 13,1% случаев (для наших случайных трёх байт).
- Про оставшиеся почти 87% случаев промолчу.
- Однако, максимум лишней информации (самое неудачное сжатие) – всего 147,42%. Чуть обогнали ЕдРо.
И выложу таблицу в Excel, где всё это считал: xlsx, pdf
:-*
Спасибо, ставлю ЛОЙС.
Спасибо за отчет, автор!
Очень познавательно, спасибо!
Процесс можно было бы значительно ускорить, просто домножая дробь на увеличивающееся число. Если результат целый — цель достигнута.
Не совсем понял, но, думаю, подразумевается, что дробь должна быть точно равна десятичному представлению в байтах?
Тогда нет, так как частное должно округляться
я толком ничего немогу понять где сжатие говрица
говрица после сжатие так сжать нелзя никак посколько кабинации вариции нелзя некак так улужить так можно сжать только состоящию из пару ч. повторную информацию ну где всетаки этот алгоритм
фильмы размером 2ГБ до 2-3 кБ
Рассмотрим три байта: 236, 82, 219. В десятичной системе я их записал так: 0.14373612. Теперь найдём два числа: это 3948 и 27467, их частное равно 0.143736119707285, что прекрасно округляется. Но! Степень сжатия тут около 111,218%.
я толком ничего немогу понять где сжатие 1 сьели только нечего недало
толком ничего непонятно и откуда 3641.
Дробь ведь уже известна. Насколько я всё это понял, дробь известна уже до последнего знака. В таком случае, домножаем эту дробь на целое, увеличивающееся на каждой итерации. Если результат — целое или имеет дробную часть меньше n*0.5e-9 или больше 1-n*0.5e-9, то числа — искомые.
Понимаете, при таком раскладе товарищу Алексею пришлось бы найти алгоритм Евклида для поиска НОД, иначе числа бы не скукоживались а наоборот, тут уж никак не скроешь про*банный школьный курс алгебры и информатики.
На самом деле проще из 2Gb фильма высчитывать контрольную сумму — а для распаковки брутфорсить её. Если получился не ожидаемый фильм (коллизия) — то продолжать брутфорс. По идее любые данные поместятся в md5, sha2 или crc — да в конце концов и до бита сжать можно.
У хеш-функций могут быть коллизии, и Ваш брутфорс выдаст совсем не то, что вы запаковали, хотя хеш будет совпадать из-за коллизии. Ничего не получиться.
Хм… А что если использовать две разные хэш-функции (например, MD5 и SHA256) и еще и сверять при этом размер начального конечного файла? Ну а на счет коллизии — вести брут до конца, создавая файл за файлом, а после просто вручную выбрать подходящий. Ну или хранить первые байты файла, чтобы снизить количество мусора. Короче, реализовать это можно, не проблема. Другое дело что каждый байт при бруте будет в геометрической прогрессии увеличивать время, нужное на расшифровку файла. Так, файл размером 1 байт в один поток расшифровывается за ~17 секунд. 2 байта — уже почти 5 минут. А 3 байта уже почти полтора часа. Поэтому это нецелесообразно. А учитывая большое количеством мусора, генерируемое подобным «архиватором» от этой идеи лучше отказаться.
Этот алгоритм специально предназначен для сжатия редкого типа файлов, которыми пользуется только сам Бабушкин для тестирования своего алгоритма сжатия… 😀