[предыдущий пост по теме: Алгоритм архивации Бабушкина]
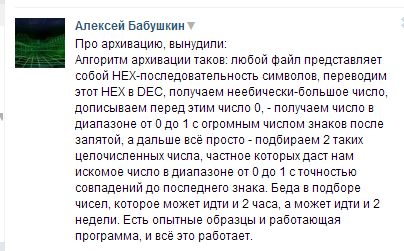
Короче, надоело мне ждать цикл в 10^14 итераций (напомню, что это для сжатия 6 байт). Долго. Немного переписал программу: сделал для трёх байт и учёл ещё одно условие, на которое не сильно обратил внимание в тот раз.
Вот пишете, что перебор в принципе не нужен, достаточно заметить, что дробь a/b, где a – двухгигабайтный фильм, а b – десять в какой-то очень большой степени, может сократиться только на 2 и на 5 (не по одному разу, конечно). Поэтому достаточно поделить оба числа на наибольший общий делитель, и дело с концом.
Небольшая оговорка: два числа (которые я уже обозвал в предыдущем посте, как m и n) не обязательно при делении должны выдавать всё наше исходное число: оно должно получаться при округлении результата до определённого знака.
Рассмотрим три байта: 236, 82, 219. В десятичной системе я их записал так: 0.14373612. Теперь найдём два числа: это 3948 и 27467, их частное равно 0.143736119707285, что прекрасно округляется. Но! Степень сжатия тут около 111,218%.